Flux cost minimization

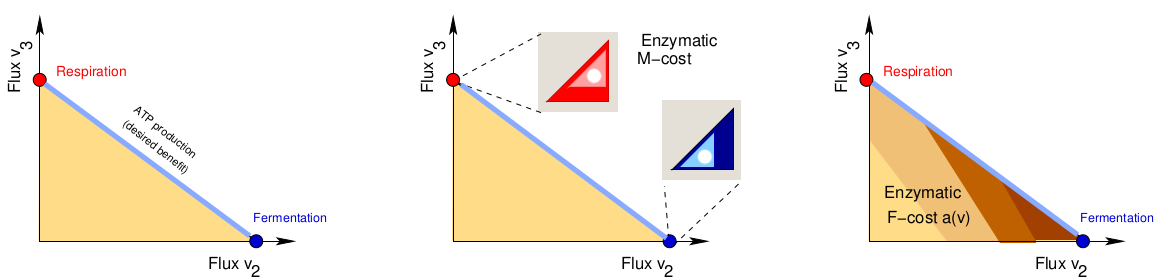
Some flux balance analysis methods score metabolic fluxes by flux costs which are then bounded or minimised during optimisation. However, linear cost functions are not very realistic. Here I derive nonlinear flux costs, representing enzyme and metabolite costs in kinetic models, and discuss their mathematical properties. The enzyme-based flux cost is defined as the minimal enzyme cost at which a given flux can be realised within a given kinetic model. Such flux costs are concave functions on the flux polytope: they scale linearly with the flux distribution and are strictly concave between flux distributions that require different optimal metabolite profiles. Minimising these costs at a given flux benefit yields a generalised, nonlinear version of FBA, and with strictly concave flux costs, the resulting optimal flux profiles will be vertices of the flux polytope. With a single flux bound (i.e., a fixed nutrient uptake or biomass production), all these vertices are elementary flux modes. With two or more flux bounds, also non-elementary flux modes may be optimal. A bound on respiration capacity, for example, can give rise to respiro-fermentation as performed by yeast and cancer cells. Cells with strictly concave flux cost functions may reduce their enzyme cost running metabolic fluxes in alternation or in separate cell compartments. Flux cost functions can also capture metabolite costs and allow for simple linear and nonlinear approximations, which justify the use of weighted flux minimisation in FBA.

Read more:

Details on flux cost functions
Details on rate / yield tradeoffs