



Next: Die atomare Dekoration der
Up: Elsers Strukturmodell
Previous: Wie sich die Cluster
Wir betrachten im weiteren Verlauf nur diejenigen Mackaycluster, die
auf den Vertizes zentriert sind. Mit der Wahl, daß die
Bergmancluster an den ungeraden Vertizes eines  -skalierten
Tilings sitzen sollen, fallen die Punkttypen
-skalierten
Tilings sitzen sollen, fallen die Punkttypen 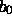 ,
, 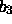 ,
,
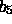 ,
, 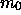 ,
, 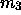 ,
, 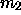 und
und 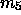 bezüglich der
hochdimensionalen Untergitter in folgende Klassen:
bezüglich der
hochdimensionalen Untergitter in folgende Klassen:
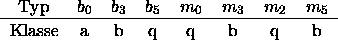
Punkte der Klasse c kommen nicht vor. In meiner Notation kann ein
Punkt verschiedenen Punkttypen angehören, wenn er Bestandteil eines
Bergman- und gleichzeitig eines Mackayclusters ist. Elser vermeidet
in seiner Notation die Zugehörigkeit eines Punktes zu zwei Typen,
indem er auch für die Bezeichnung der Punkte Dominanz der
Bergmancluster vorschreibt. Ein 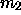 -Punkt, der gleichzeitig
-Punkt, der gleichzeitig
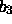 ist, heißt bei ihm
ist, heißt bei ihm 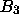 . Ich verwende zur
Unterscheidung für Elsers Notation Großbuchstaben und für meine
Notation Kleinbuchstaben. Im einzelnen gilt für die Quasigitter der
Punkttypen:
. Ich verwende zur
Unterscheidung für Elsers Notation Großbuchstaben und für meine
Notation Kleinbuchstaben. Im einzelnen gilt für die Quasigitter der
Punkttypen:

