



Next: Graphen und ihr Spektrum
Up: Elektronen in isolierten Metallclustern
Previous: Elektronen in isolierten Metallclustern
Die Molekülorbitale eines Clusters sollen näherungsweise in einer Basis
atomarer s-Orbitale entwickelt werden. Aus Forderung minimaler Energie
für den Grundzustand folgt eine Eigenwertgleichung für die
Entwicklungskoeffizienten 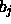 :
:

mit Hamiltonmatrix 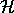 und Überlappmatrix
und Überlappmatrix 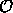 .
.
Die Überlappmatrix wird als Identitätsmatrix angenommen oder durch
eine Löwdin-Orthogonalisierung dazu gemacht, und an die
Hamiltonmatrix stellen wir drei weitere Forderungen:
- Die Diagonalelemente (``on-site-Energien'') haben einen festen Wert E
- Die Matrixelemente zwischen Nachbaratomen (``Hüpfelemente'')
haben einen festen Wert h
- Alle übrigen Matrixelemente verschwinden
Durch einfache Umskalierung lassen sich stets die on-site-Energie E=0
und h=1 setzen, und man erhält die Inzidenzmatrix eines Graphen,
deren Eigenwerte jetzt betrachtet werden. Die starke Vereinfachung
des physikalischen Bildes zahlt sich aus in Form von Theoremen, die
ohne Rücksicht auf die chemischen Elemente oder die genauen
Bindungsabstände die reine Topologie des Moleküls mit dem
Einelektronenspektrum in Verbindung bringen. Die Methode läßt sich
auf Matrizen mit unterschiedlichen Arten von Hüpfelementen 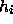 erweitern. Um allerdings unter Berücksichtigung der jeweiligen
chemischen Elemente realistische Spektren oder Energiebeiträge zu
berechnen, müßte man p- und d- Zustände mit in die Basis aufnehmen.
Danach steht und fällt die Qualität der Ergebnisse im wesentlichen
mit einer guten Bestimmung der Matrixelemente.
erweitern. Um allerdings unter Berücksichtigung der jeweiligen
chemischen Elemente realistische Spektren oder Energiebeiträge zu
berechnen, müßte man p- und d- Zustände mit in die Basis aufnehmen.
Danach steht und fällt die Qualität der Ergebnisse im wesentlichen
mit einer guten Bestimmung der Matrixelemente.
![]() :
:
![]()
![]() und Überlappmatrix
und Überlappmatrix ![]() .
.