Der goldene Schnitt ist definiert als positive Lösung der Gleichung
. ist irrational, da aus 
mit ungeradem p
oder q 
folgen würde, p und q also
gerade sein müssen - im Widerspruch zur Voraussetzung.
Es gilt
, 
sowie die
Kettenbruchdarstellung
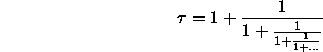
denn dieser Ausdruck erfüllt 
und damit .
Aus der Kettenbruchdarstellung folgt eine Approximation durch Quotienten
aufeinanderfolgender Fibonaccizahlen 
mit
, 
und 
Ganzzahlige Potenzen 
und
mit 
lassen sich stets folgendermaßen zerlegen:
