Next: Die adiabatische Näherung
Up: Die Behandlung von Elektronensystemen
Previous: Die Behandlung von Elektronensystemen
Moleküle und Festkörper werden quantenmechanisch durch
Vielteilchenwellenfunktionen für Kerne und Elektronen beschrieben:
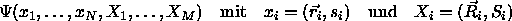
Dabei bezeichnen 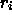 und
und 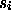 mögliche Positionen und
Spinquantenzahlen für die Elektronen,
mögliche Positionen und
Spinquantenzahlen für die Elektronen, 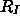 und
und 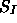 entsprechend
für die Kerne: Die Gesamtheit dieser Wellenfunktionen bilden einen
Hilbertraum. Tatsächlich benötigt wird nur der Unterraum der
Wellenfunktionen, die symmetrisch/antisymmetrisch gegen Austausch
ununterscheidbarer Teilchen mit
ganzzahligem/halbzahligem Spin sind.
entsprechend
für die Kerne: Die Gesamtheit dieser Wellenfunktionen bilden einen
Hilbertraum. Tatsächlich benötigt wird nur der Unterraum der
Wellenfunktionen, die symmetrisch/antisymmetrisch gegen Austausch
ununterscheidbarer Teilchen mit
ganzzahligem/halbzahligem Spin sind.
Die zeitliche Entwicklung eines reinen Zustandes im Schrödingerbild
ist bestimmt durch den Hamiltonoperator H:

Er läßt sich als Summe der kinetischen Energie, der äußeren
potentiellen Energie (Einteilchenoperatoren)
und der betrachteten Wechselwirkungsenergien (Zweiteilchenoperatoren)
schreiben, im Falle reiner Coulomb-Wechselwirkung:
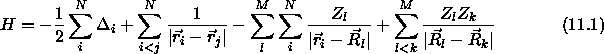
Wir sind in erster Linie an Eigenschaften des
Grundzustandes interessiert, insbesondere an der totalen Energie, dem
niedrigsten Eigenwert des Hamiltonoperators.
Bei endlicher Temperatur T und fester Teilchenzahl wird das System als
quantenstatistisches kanonisches Ensemble mit Dichteoperator 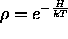 beschrieben, indem man
die Erwartungswerte von Observablen O als
beschrieben, indem man
die Erwartungswerte von Observablen O als 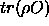 ausdrückt. Die
Spur läuft dabei über alle (N+M)-Teilchenwellenfunktionen.
ausdrückt. Die
Spur läuft dabei über alle (N+M)-Teilchenwellenfunktionen.