



Next: Bestimmung der DOS und
Up: Die LMTO-ASA-Methode
Previous: Die atomic sphere appoximation
Als Ausgangsdaten werden aus der Zellgeometrie geeignete Leerkugeln und
Kugelradien sowie die Strukturkonstanten bestimmt.
Die Rechnung beginnt mit einem geschätzten
Potential, das in die ``muffin tin''-Form
gebracht wird. Um Selbstkonsistenz zu erreichen, werden aus
dem Potential Elektronenzustände bestimmt, die über die
Ladungsdichte der besetzten Zustände auf ein neues Potential führen.
Dieser Vorgang wiederholt sich iterativ so lange, bis altes und neues
Potential beziehungsweise Ladungsdichte hinreichend gut übereinstimmen.
Zunächst werden durch numerische Lösung der radialen
Schrödingergleichung (mit entsprechenden DF-Termen) die
Zustände der inneren (``core-'') Elektronen
bestimmt, die im Rahmen der Näherung keine Hybridisierung eingehen.
Zur Berechnung der Valenz- bzw.
Leitungszustände wird für jedes Atom und jede
Drehimpulsquantenzahl l die energieabhängige Lösung der radialen
Schrödingergleichung nach einem gewissen 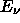 entwickelt und durch
vier Potentialparameter charakterisiert. Als Basis für die
Einelektronenzustände dienen Blochsummen dieser Lösungen.
entwickelt und durch
vier Potentialparameter charakterisiert. Als Basis für die
Einelektronenzustände dienen Blochsummen dieser Lösungen.
Für jeden Blochvektor 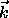 ergibt sich eine
Säkularmatrix, die durch die Potentialparameter und die
Strukturkonstanten bestimmt ist. Die Diagonalisierung liefert
Energiewerte und Zustände für jeweils ein
ergibt sich eine
Säkularmatrix, die durch die Potentialparameter und die
Strukturkonstanten bestimmt ist. Die Diagonalisierung liefert
Energiewerte und Zustände für jeweils ein 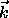 . Nun wird eine
kleine Anzahl von
. Nun wird eine
kleine Anzahl von 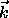 -Vektoren verwendet, um durch eine
numerische Integration über die Brillouinzone die aus der Besetzung
der Zustände bis
-Vektoren verwendet, um durch eine
numerische Integration über die Brillouinzone die aus der Besetzung
der Zustände bis 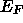 resultierende Ladungsdichte zu bestimmen.
Diese wird nach den Basisfunktionen entwickelt und durch die
Koeffizienten (``Momente'') charakterisiert. Aus den Core- und
Valenzladungsdichten wird schließlich ein neues effektives Potential
berechnet, das der Ausgangspunkt des nächsten großen
Iterationsschrittes bildet.
resultierende Ladungsdichte zu bestimmen.
Diese wird nach den Basisfunktionen entwickelt und durch die
Koeffizienten (``Momente'') charakterisiert. Aus den Core- und
Valenzladungsdichten wird schließlich ein neues effektives Potential
berechnet, das der Ausgangspunkt des nächsten großen
Iterationsschrittes bildet.