Next: Spektren ikosaedrischer Graphen
Up: Elektronen in isolierten Metallclustern
Previous: Graphen und ihr Spektrum
Das Momentetheorem für Tight-Binding-Modelle geht auf Friedel sowie
Cyrot-Lackmann zurück. Ich folge der Darstellung in [Pettifor].
Die Verteilung der Eigenwerte 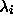 eines Graphen G (bei
Entartung werden Eigenwerte hier mehrfach gezählt) läßt sich
charakterisieren durch ihre Momente
eines Graphen G (bei
Entartung werden Eigenwerte hier mehrfach gezählt) läßt sich
charakterisieren durch ihre Momente 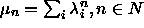 . In diesem Fall sind dies gleichzeitig die zentralen Momente.
. In diesem Fall sind dies gleichzeitig die zentralen Momente.
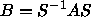 sei diagonal, j indiziere die kanonischen
Basiszustände des Vektorraums von G, i indiziere eine Menge
linear unabhängiger Eigenzustände von A. Dann läßt sich das n-te
Moment folgendermaßen umschreiben:
sei diagonal, j indiziere die kanonischen
Basiszustände des Vektorraums von G, i indiziere eine Menge
linear unabhängiger Eigenzustände von A. Dann läßt sich das n-te
Moment folgendermaßen umschreiben:
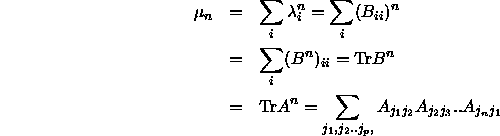
Es ist also in erster Linie die Spur über die n-te Potenz der
Inzidenzmatrix, die sich für diese Matrizen durch geschlossene Pfade
ausdrücken läßt: Das n-te Moment 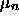 ist also bestimmt durch
die Anzahl geschlossener Pfade
ist also bestimmt durch
die Anzahl geschlossener Pfade 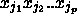 der Länge n
auf G. Durch Abzählen solcher Pfade lassen sich Eigenschaften des
Spektrums bestimmen. Das nullte Moment
der Länge n
auf G. Durch Abzählen solcher Pfade lassen sich Eigenschaften des
Spektrums bestimmen. Das nullte Moment 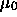 ergibt die Anzahl der
Vertizes, also auch der Eigenwerte (bei Entartung wieder mehrfach
gezählt). Weiter betrachtet man am besten die normierten Momente
ergibt die Anzahl der
Vertizes, also auch der Eigenwerte (bei Entartung wieder mehrfach
gezählt). Weiter betrachtet man am besten die normierten Momente
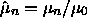 . Das erste normierte Moment ist die mittlere
on-site-Energie, in diesem Fall 0.
. Das erste normierte Moment ist die mittlere
on-site-Energie, in diesem Fall 0. 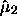 , die Varianz
des Spektrums, ist gegeben durch die mittlere Zahl der 2-Pfade, also
den mittleren Grad von G (die Koordinationszahl).
, die Varianz
des Spektrums, ist gegeben durch die mittlere Zahl der 2-Pfade, also
den mittleren Grad von G (die Koordinationszahl). 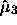 , die
Schiefe des Spektrums, ergibt sich aus den geschlossenen
3-Pfaden, und
, die
Schiefe des Spektrums, ergibt sich aus den geschlossenen
3-Pfaden, und
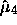 , die Bimodalität, aus den geschlossenen 4-Pfaden.
, die Bimodalität, aus den geschlossenen 4-Pfaden.
Leider ist eine Funktion erst durch die Angabe aller Momente eindeutig
bestimmt. Um von wenigen bekannten Momenten auf die DOS zu schließen,
kann man an die DOS die Forderung maximaler Entropie stellen und die
bekannten Momente als Nebenbedingungen betrachten.
Dies führt bei Vorgabe von N Momenten auf die Form 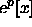 mit einem Polynom Nter Ordung p[x], ein Problem, das nur
numerisch gelöst werden kann.
mit einem Polynom Nter Ordung p[x], ein Problem, das nur
numerisch gelöst werden kann.