Mit der bereitgestellten Methode sollen nun Spektren für die Cluster
der Elsermodells bestimmt werden: in den Graphen entsprechen die
Vertizes Atomen, die Kanten den Bindungen, also kurzen Abständen
![]() ,
, ![]() oder
oder ![]() .
Spektren derartiger Graphen sind in den Abbildungen
6.1 und 6.2 zu sehen. Die
Eigenwerte von Ikosaeder und Dodekaeder wurden exakt durch
Diagonalisierung der kollabierten Inzidenzmatrix bestimmt, die
Multiplizitäten folgten unter Zuhilfenahme des Momentetheorems. Als
Eigenwerte findet man
.
Spektren derartiger Graphen sind in den Abbildungen
6.1 und 6.2 zu sehen. Die
Eigenwerte von Ikosaeder und Dodekaeder wurden exakt durch
Diagonalisierung der kollabierten Inzidenzmatrix bestimmt, die
Multiplizitäten folgten unter Zuhilfenahme des Momentetheorems. Als
Eigenwerte findet man
![]() [3fach], -1[5],
[3fach], -1[5], ![]() [3fach], 5 [1fach] für den
Ikosaeder sowie
[3fach], 5 [1fach] für den
Ikosaeder sowie
![]() [3fach], -2[4fach], 0 [4fach],
1 [5fach],
[3fach], -2[4fach], 0 [4fach],
1 [5fach], ![]() [3fach] 3 [1fach]
für den Dodekaeder. Die übrigen Spektren wurden
durch numerische Diagonalisierung der Inzidenzmatrizen berechnet.
[3fach] 3 [1fach]
für den Dodekaeder. Die übrigen Spektren wurden
durch numerische Diagonalisierung der Inzidenzmatrizen berechnet.
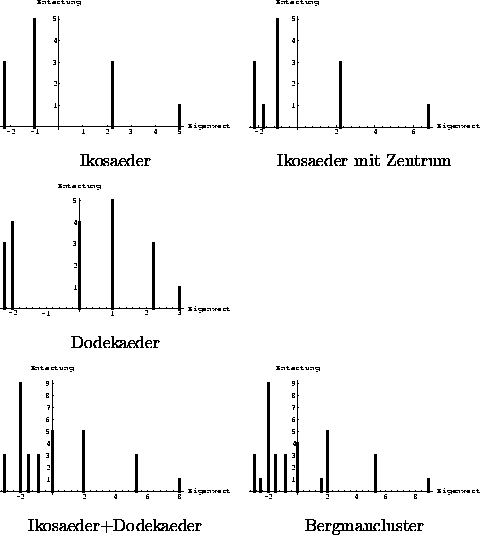
Abbildung: Multiplizitäten der Eigenwerte von Bergman-Graphen:
die Eigenwerte entsprechen negativen Energien
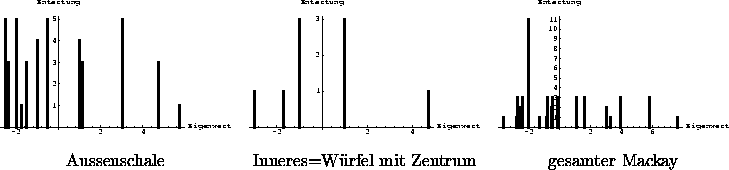
Abbildung 6.2: Eigenwerte von Mackay-Graphen
An den Spektren fällt Verschiedenes auf: Die Multiplizitäten der
ikosaedersymmetrischen Graphen, 1, 3, 4 und 5, entsprechen den
Dimensionen der Darstellungen der Ikosaedergruppe (siehe Anhang
A). Da alle Graphen ungeradzahlige geschlossene
Pfade enthalten, ist keines der Spektren spiegelsymmetrisch. Die
Spektren von Ikosaeder und Dodekaeder lassen sich gut vergleichen:
wegen der höheren Koordinationszahl ist das Spektrum des Ikosaeders
stärker aufgeweitet als das des Dodekaeders. Dieser hat, wegen der
verschwindenden 3-Pfade ein relativ symmetrisches Spektrum. Erst die
5-Pfade sorgen für die Asymmetrie (in Form einer größeren Lücke).
Das Spektrum des Ikosaeders dagegen fällt von links nach rechts ab.
Beim Kombinieren zweier Graphen überlagern sich deren Spektren, und
die zusätzlichen Kanten wirken als kleine Störung, die Zustände
gleichen Drehimpulscharakters (erkennbar an der Mulitplizität)
koppelt. Dies ist an den Spektren Ikosaeder+Dodekaeder und
Bergmancluster schön zu sehen. Hier treten außerdem noch zufällige
Entartungen auf.
Beim Vergleich mit realistischen Molekülspektren muß man sich
vergegenwärtigen, daß die Hüpfelemente in der Hamiltonmatrix vom
Überlapp der Wellenfunktionen mit einem negativen effektiven
Potential herrühren, also negative Werte haben, im Gegensatz zu den
Elementen der Inzidenzmatrix, die nach Definition h=1 betragen. In den
Schaubildern ist sozusagen die negative
Energie aufgetragen.
Um aus den Spektren einfachste Schätzwerte für ``bond''-Energien
(siehe [Pettifor], Kapitel 4) zu gewinnen, ist eine Annahme über
die Besetzungszahl nötig. Wenn jedes Atom ein Elektron beiträgt,
zwei Elektronen in ein MO passen und das Hüpfelement h=-1 eins
beträgt, ergeben sich für die Beispiele bei Besetzung der untersten
Zustände die folgenden Energien pro Atom:
