



Next: Koordinaten zum Elsermodell
Up: Sammelsurium zur ikosaedrischen Geometrie
Previous: Die Ikosaedergruppe
In [Baa90] und [Kra91] wird eine cut and project-Methode zur
Erzeugung nichtperiodischer Tilings verwendet, die sich nicht nur auf
Vertizes, sondern auch auf die Tiles und ihre verschiedendimensionalen
Begrenzungen bezieht. Um die Verwendung des Triakontaeders als
Fenster für die ikosaedrischen
Tilings zu begründen, liefere ich hier eine knappe Beschreibung:
Man beginnt mit einem kubischen Gitter 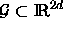 .
Die Voronoizelle (auch: ``Wigner-Seitz-Zelle'')
.
Die Voronoizelle (auch: ``Wigner-Seitz-Zelle'') 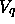 zum
Gitterpunkt q ist die Menge aller Punkte, deren Abstand von q
kleiner oder gleich dem Abstand von irgendeinem anderen Gitterpunkt
ist. Bei einem primitiv-kubischen Gitter ist die Voronoizelle ein
2d-dimensionaler Hyperkubus, und die p-Begrenzungen sind jeweils
p-dimensionale Hyperkuben, also Punkte, Strecken, Quadrate, Würfel
bzw. Hyperkuben. Bei anderen Gittern sind die Formen komplizierter.
Die Voronoizellen zu
benachbarten Gitterpunkten haben gemeinsame Begrenzungen.
zum
Gitterpunkt q ist die Menge aller Punkte, deren Abstand von q
kleiner oder gleich dem Abstand von irgendeinem anderen Gitterpunkt
ist. Bei einem primitiv-kubischen Gitter ist die Voronoizelle ein
2d-dimensionaler Hyperkubus, und die p-Begrenzungen sind jeweils
p-dimensionale Hyperkuben, also Punkte, Strecken, Quadrate, Würfel
bzw. Hyperkuben. Bei anderen Gittern sind die Formen komplizierter.
Die Voronoizellen zu
benachbarten Gitterpunkten haben gemeinsame Begrenzungen.
Zu jeder Begrenzung einer Voronoizelle ist ein duales Objekt
definiert: Seien 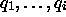 Gitterpunkte, deren
Voronoizellen eine gemeinsame p-Begrenzung P haben, so ist das zu
P duale Objekt
Gitterpunkte, deren
Voronoizellen eine gemeinsame p-Begrenzung P haben, so ist das zu
P duale Objekt 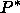 definiert als die konvexe Hülle dieser
Gitterpunkte. P und
definiert als die konvexe Hülle dieser
Gitterpunkte. P und 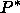 schneiden sich in genau einem Punkt,
und die Summe ihrer Dimensionen ergibt 2d. Die dualen Objekte zu
den Ecken der Voronoizellen heißen Delonezellen. Jedes Gitter
definiert also einen Komplex von Voronoizellen und einen Komplex von
dazu dualen
Delonezellen.
schneiden sich in genau einem Punkt,
und die Summe ihrer Dimensionen ergibt 2d. Die dualen Objekte zu
den Ecken der Voronoizellen heißen Delonezellen. Jedes Gitter
definiert also einen Komplex von Voronoizellen und einen Komplex von
dazu dualen
Delonezellen.
Jetzt wenden wir die bekannte cut-and-project-Methode im Bild der
atomaren Hyperflächen an. Im besonderen Fall der ikosaedrischen
Tilings mit d=3 betrachten wir den Schnittraum 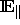 (siehe
Abschnitt 2). Verläuft der Schnitt durch eine 6-,
5-, 4- oder 3-dimensionale Voronoibegrenzung (``Hyperfläche''), so
wird die dazu duale Begrenzung projiziert. Als Bilder unter der
Projektion ergeben sich die Tiles, ihre Flächen, Kanten und Vertizes.
Das Triakontaeder als Projektion des sechsdimensionalen Hyperwürfels
nach
(siehe
Abschnitt 2). Verläuft der Schnitt durch eine 6-,
5-, 4- oder 3-dimensionale Voronoibegrenzung (``Hyperfläche''), so
wird die dazu duale Begrenzung projiziert. Als Bilder unter der
Projektion ergeben sich die Tiles, ihre Flächen, Kanten und Vertizes.
Das Triakontaeder als Projektion des sechsdimensionalen Hyperwürfels
nach 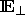 codiert deshalb die Vertizes, also die nulldimensionalen
Begrenzungen des Rhomboedertilings. Die Rollen von Voronoi- und
Delonezellen können bei der Konstruktion auch vertauscht werden, um
ein anderes Tiling zu erhalten.
codiert deshalb die Vertizes, also die nulldimensionalen
Begrenzungen des Rhomboedertilings. Die Rollen von Voronoi- und
Delonezellen können bei der Konstruktion auch vertauscht werden, um
ein anderes Tiling zu erhalten.




Next: Koordinaten zum Elsermodell
Up: Sammelsurium zur ikosaedrischen Geometrie
Previous: Die Ikosaedergruppe