Für die Einbettung der Ikosaedergruppe in die hyperoktaedrische
Gruppe des ![]() wählen wir als Basisvektoren sechs unabhängige Ecken
des Ikosaeders, wie in Abbildung 2.5 gezeigt.
wählen wir als Basisvektoren sechs unabhängige Ecken
des Ikosaeders, wie in Abbildung 2.5 gezeigt.
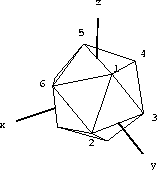
Abbildung 2.5: Die ikosaedrischen Basisvektoren ![]()
Bezüglich dieser Einbettung der Ikosaedergruppe zerfällt der ![]() in zwei dreidimensionale invariante Unterräume
in zwei dreidimensionale invariante Unterräume ![]() und
und ![]() , von
denen
, von
denen ![]() als
physikalischer Raum gedeutet wird.
als
physikalischer Raum gedeutet wird.
Aus der Wahl der Basisvektoren folgen die Projektoren in die
Unterräume ![]() und
und ![]() . Bei Einschränkung auf ein kubisches
Gitter
. Bei Einschränkung auf ein kubisches
Gitter ![]() sind diese Abbildungen bijektiv,
ebenso die Abbildung
sind diese Abbildungen bijektiv,
ebenso die Abbildung ![]() von
von ![]() nach
nach ![]() .
.
Wir betrachten im folgenden das sechsdimensionale
hyperkubisch-raumzentrierte Gitter. Es zerfällt in das Untergitter
![]()
und die drei Nebenklassen bezüglich ![]() :
:
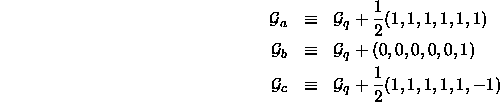
![]() kann als ``flächenzentriert'' mit Kantenlänge 2
gedeutet werden und trägt in anderen Arbeiten die Namen
kann als ``flächenzentriert'' mit Kantenlänge 2
gedeutet werden und trägt in anderen Arbeiten die Namen ![]() oder
2F-Gitter. Die Vereinigung von
oder
2F-Gitter. Die Vereinigung von ![]() und
und ![]() ergibt das primitive Gitter mit Kantenlänge 1. Die vier Gitter
ergibt das primitive Gitter mit Kantenlänge 1. Die vier Gitter
![]() werden durch
werden durch ![]() (
(![]() ) jeweils
bijektiv auf einen 2F-Modul
) jeweils
bijektiv auf einen 2F-Modul ![]() (
(![]() ) abgebildet. Alle vier Moduln besitzen die volle
Ikosaedersymmetrie (Punktgruppe
) abgebildet. Alle vier Moduln besitzen die volle
Ikosaedersymmetrie (Punktgruppe ![]() ). Sie haben paarweise
verschwindende Schnittmengen. Der Modul
). Sie haben paarweise
verschwindende Schnittmengen. Der Modul ![]() ist
invariant gegenüber Skalierung um
ist
invariant gegenüber Skalierung um ![]() , die anderen drei werden
durch
, die anderen drei werden
durch ![]() -Skalierung (siehe Anhang A)
folgendermaßen aufeinander abgebildet:
-Skalierung (siehe Anhang A)
folgendermaßen aufeinander abgebildet:
![]()
![]() -Skalierung im physikalischen Raum wirkt sich im internen Raum
als
-Skalierung im physikalischen Raum wirkt sich im internen Raum
als ![]() -Skalierung aus. Die Klassenzugehörigkeit der Summe oder
Differenz von Punkten ergibt sich aus der
Klassenaddition +:
-Skalierung aus. Die Klassenzugehörigkeit der Summe oder
Differenz von Punkten ergibt sich aus der
Klassenaddition +:
Um die ikosaedrischen F-Phasen-Quasikristalle zu modellieren, werden
wir, von einem Untergitter ausgehend, Fenster für drei der
Untergitter konstruieren. Die Struktur ergibt sich dann als
Vereinigung der drei mit diesen Fenstern erzeugten Unterquasigitter