



Next: Das Hartree-Fock-Verfahren
Up: Die Behandlung von Elektronensystemen
Previous: Die adiabatische Näherung
Es bringt für
Vielteilchenprobleme eine große Vereinfachung mit sich, wenn die
Zweiteilchen-Wechselwirkung (Zweiteilchenterme im Hamiltonoperator)
näherungsweise durch ein effektives Potential (einen
Einteilchenterm) nachgeahmt werden kann. Ein System
wechselwirkender Teilchen in einem äußeren Potential V wird so
durch ein Referenzsystem nichtwechselwirkender Teilchen in einem
modifizierten mittleren Potential 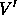 ersetzt.
ersetzt.
Das Problem N nichtwechselwirkender Spin-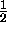 -Teilchen in
einem äußeren Potential ist nämlich vergleichsweise einfach zu
lösen: der Grundzustand ist einfach das antisymmetrisierte Produkt
(die Slaterdeterminante) der N untersten Einteilchenzustände in
diesem Potential. Das Problem nichtwechselwirkender Teilchen ist damit
äquivalent zu einem Einteilchenproblem mit Einteilchenhamiltonoperator h.
-Teilchen in
einem äußeren Potential ist nämlich vergleichsweise einfach zu
lösen: der Grundzustand ist einfach das antisymmetrisierte Produkt
(die Slaterdeterminante) der N untersten Einteilchenzustände in
diesem Potential. Das Problem nichtwechselwirkender Teilchen ist damit
äquivalent zu einem Einteilchenproblem mit Einteilchenhamiltonoperator h.
Eine wichtige Einteilchengröße ist die
totale Zustandsdichte (auch DOS, für ``density of states''): dies ist eine
Distribution, die für ein System die Einteilchenergien und ihre
Multiplizitäten angibt. Sie ist definiert als
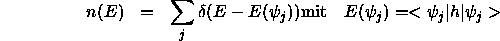
Hier soll j alle Einteilchenzustände 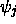 indizieren.
Die DOS wird gerne näherungsweise als eine stetige Funktion betrachtet.
indizieren.
Die DOS wird gerne näherungsweise als eine stetige Funktion betrachtet.
Bei endlicher Temperatur T ist für das nichtwechselwirkende
Referenzsytem die Besetzungswahrscheinlichkeit eines Zustandes durch
die Fermi-Dirac-Verteilung

gegeben. Das chemische Potential 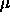 ist für jede Temperatur durch die
vorgegebene Teilchenzahl N bestimmt:
ist für jede Temperatur durch die
vorgegebene Teilchenzahl N bestimmt:
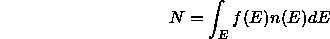
Die Fermienergie 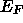 ist das chemische Potential für T=0 und
liegt in der Mitte zwischen dem obersten besetzten und dem untersten
unbesetzten Zustand.
ist das chemische Potential für T=0 und
liegt in der Mitte zwischen dem obersten besetzten und dem untersten
unbesetzten Zustand.
Obwohl die Einteilchen-DOS nur im Rahmen der Einteilchennäherung
überhaupt definiert ist, nimmt sie in der Festkörperphysik eine
zentrale Stellung ein: Viele Transporteigenschaften von Festkörpern,
lassen sich in einer groben Näherung auf die
Einteilchenzustandsdichte im Bereich der Fermikante zurückführen.
Zudem liefert die DOS mit der Bandstrukturenergie, dem
''Energieschwerpunkt'' unterhalb 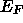 , einen entscheidenden Beitrag
zur gesamten Strukturenergie und hat damit wesentlichen Einfluß
auf die Stabilität von Strukturen.
, einen entscheidenden Beitrag
zur gesamten Strukturenergie und hat damit wesentlichen Einfluß
auf die Stabilität von Strukturen.