



Next: Dichtefunktionalmethoden
Up: Die Behandlung von Elektronensystemen
Previous: Reduktion des Vielteilchenproblems auf
Eine Möglichkeit, effektive Einteilchengleichungen zu erhalten, ist
das Hartree-Fock-Verfahren. Hier betrachtet man nur solche
antisymmetrischen
Vielteilchenwellenfunktionen, die sich als einzelne Slaterdeterminaten
ausdrücken lassen: 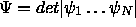 . Unter diesen
Zuständen sucht man denjenigen mit der geringsten Energie
(Erwartungswert des Vielteilchenhamiltonoperators) unter der
Nebenbedingung, daß der zugehörige Satz von Einteilchenwellenfunktionen
. Unter diesen
Zuständen sucht man denjenigen mit der geringsten Energie
(Erwartungswert des Vielteilchenhamiltonoperators) unter der
Nebenbedingung, daß der zugehörige Satz von Einteilchenwellenfunktionen
 orthonormiert
sein soll. Diese Variationsrechnung führt auf Gleichungen für die
Einteilchenzustände, welche die gesuchte Slaterdeterminante bilden.
Diese Hartree-Fock-Gleichungen haben die Form von
Einteilchenschrödingergleichungen mit einem modifizierten Potential.
Da dieses effektive Potential selbst von der Ladungsdichte bzw. den
orthonormiert
sein soll. Diese Variationsrechnung führt auf Gleichungen für die
Einteilchenzustände, welche die gesuchte Slaterdeterminante bilden.
Diese Hartree-Fock-Gleichungen haben die Form von
Einteilchenschrödingergleichungen mit einem modifizierten Potential.
Da dieses effektive Potential selbst von der Ladungsdichte bzw. den
 abhängt, müssen
Ladungsdichte und Potential selbstkonsistent bestimmt werden.
Praktisch löst man das Problem iterativ: Man beginnt beispielsweise
mit einer geschätzten Ladungsdichte, bestimmt daraus ein effektives
Potential, löst die Hartree-Fock-Gleichungen und berechnet eine neue
Ladungsdichte. Mit dieser beginnt man von neuem und wiederholt den
ganzen Vorgang so lange, bis alte und neue Ladungsdichte hinreichend
gut übereinstimmen.
abhängt, müssen
Ladungsdichte und Potential selbstkonsistent bestimmt werden.
Praktisch löst man das Problem iterativ: Man beginnt beispielsweise
mit einer geschätzten Ladungsdichte, bestimmt daraus ein effektives
Potential, löst die Hartree-Fock-Gleichungen und berechnet eine neue
Ladungsdichte. Mit dieser beginnt man von neuem und wiederholt den
ganzen Vorgang so lange, bis alte und neue Ladungsdichte hinreichend
gut übereinstimmen.
Es ist klar, daß im Hartree-Fock-Verfahren Information über das
System verlorengeht. Angeregte Zustände können beispielsweise nur
als Anregung einzelner Teilchen verstanden werden. Die Abweichungen
von den Eigenschaften des echten Vielteilchensystems, die pauschal als
Korrelationseffekte bezeichnet werden, lassen sich vermindern, indem
man im Variationsverfahren Linearkombinationen aus verschiedenen
Slaterdeterminanten zuläßt, die mit Hilfe angeregter
(``virtueller'') Einteilchenzustände gebildet werden. Allerdings
steigt dadurch auch der Rechenaufwand enorm.