Next: Behandlung von Einteilchenproblemen
Up: Dichtefunktionalmethoden
Previous: Die Grundzustandsdichte als Lösung
Kohn und Sham [Kohn65] machten den Ansatz, im
Energiefunktional 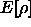 das kinetische Funktional
das kinetische Funktional 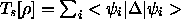 eines
nichtwechselwirkenden Referenzsystems und den Hartreeterm
zu verwenden und alle nötigen
Korrekturterme pauschal zu einem sogenannten
``Exchange-Correlation-Funktional''
eines
nichtwechselwirkenden Referenzsystems und den Hartreeterm
zu verwenden und alle nötigen
Korrekturterme pauschal zu einem sogenannten
``Exchange-Correlation-Funktional'' 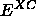 (mit unbekannter
funktionaler Abängigkeit von
(mit unbekannter
funktionaler Abängigkeit von 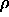 ) zusammenzufassen, das nun das
Austauschfunktional der Thomas-Fermi-Dirac-Theorie ersetzt:
) zusammenzufassen, das nun das
Austauschfunktional der Thomas-Fermi-Dirac-Theorie ersetzt:
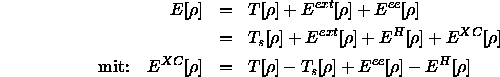
Diese Aufteilung hat den Vorteil, daß sich
Fehler in der kinetischen Energie und der
Elektron-Elektron-Wechselwirkung gegenseitig aufheben.
Levy und Lieb haben gezeigt, kann man die Variation auf
``N-darstellbare'' Grundzustandsdichten ausweiten kann: das sind solche
Dichten,
die sich also als Summe von Einteilchendichten schreiben lassen:
 . Praktisch wird die
Variation gleich über Einteilchenwellenfunktionen ausgeführt, und
zusammen mit der Forderung der Orthonormierung folgen nach einer
unitären Transformation die Kohn-Sham-Gleichungen
. Praktisch wird die
Variation gleich über Einteilchenwellenfunktionen ausgeführt, und
zusammen mit der Forderung der Orthonormierung folgen nach einer
unitären Transformation die Kohn-Sham-Gleichungen
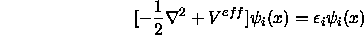
mit dem ladungsdichteabhängigen Potential
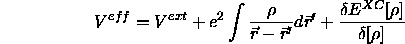
Wellenfunktionen und Potential sind wieder selbstkonsistent zu bestimmen.
Die Güte des Kohn-Sham-Verfahrens hängt entscheidend von der Wahl
des Funktionals 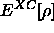 ab, das den Austauschterm der
Hartree-Fock-Theorie ersetzt: es kann beispielsweise an experimentelle
Daten angepaßt werden. Ein verbesserter Ansatz mit
Gradientenkorrektur lautet
ab, das den Austauschterm der
Hartree-Fock-Theorie ersetzt: es kann beispielsweise an experimentelle
Daten angepaßt werden. Ein verbesserter Ansatz mit
Gradientenkorrektur lautet
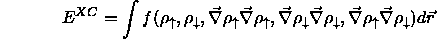
Bei Berücksichtigung des Elektronenspins s werden die
Einteilchenwellenfunktionen als Produkt aus Ortsraum- und
Spinraumfunktion 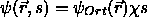 geschrieben (``restricted''). Man kann unter Umständen die Energie
noch weiter absenken, wenn für verschiedene Spinrichtungen
verschiedene Ortsraumfunktionen zugelassen werden (``unrestricted'').
Die damit gebildete Grundzustands-Slaterdeterminante ist allerdings
keine Eigenzustand zum Spinoperator mehr.
geschrieben (``restricted''). Man kann unter Umständen die Energie
noch weiter absenken, wenn für verschiedene Spinrichtungen
verschiedene Ortsraumfunktionen zugelassen werden (``unrestricted'').
Die damit gebildete Grundzustands-Slaterdeterminante ist allerdings
keine Eigenzustand zum Spinoperator mehr.