Next: Die Kohn-Sham-Theorie
Up: Dichtefunktionalmethoden
Previous: Reduzierte N-Teilchendichten
Ein erster Versuch von Thomas und Fermi zur Bestimmung der
Grundzustandsladungsdichte als Lösung eines Variationsproblems
geschah 1925: Danach soll die Minimierung eines geeigneten
Energiefunktionals 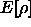 unter der Nebenbedingung
unter der Nebenbedingung 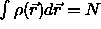 die Ladungsdichte zum Grundzustand ergeben.
Für die Bestimmung von
die Ladungsdichte zum Grundzustand ergeben.
Für die Bestimmung von 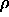 hängt jetzt alles an der unbekannten
funktionalen Abhängigkeit von
hängt jetzt alles an der unbekannten
funktionalen Abhängigkeit von 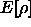 . Der Ansatz von Thomas und
Fermi für
. Der Ansatz von Thomas und
Fermi für 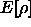 (in einer von Dirac modifizierten Version)
lautet:
(in einer von Dirac modifizierten Version)
lautet:
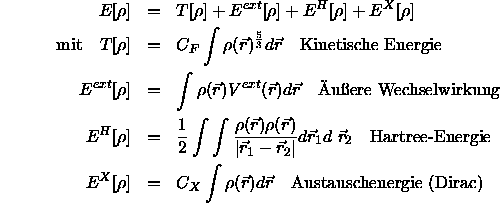
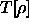 und
und 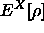 sind aus exakten Rechnungen für das freie
Elektronengas bestimmt, also ein System konstanter Dichte. Der
einfache Ansatz, Funktionale von
sind aus exakten Rechnungen für das freie
Elektronengas bestimmt, also ein System konstanter Dichte. Der
einfache Ansatz, Funktionale von 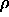 als Integrale über eine
Funktion von
als Integrale über eine
Funktion von 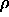 auszudrücken, wird allgemein als local
density approximation (LDA) bezeichnet.
auszudrücken, wird allgemein als local
density approximation (LDA) bezeichnet.
Dieses eher heuristische Vorgehen wurde von Hohenberg und Kohn
[Hoh64] theoretisch fundiert: sie zeigten, daß für
eine Menge von Vielteilchenhamiltonoperatoren, die sich nur im
äußeren Potential unterscheiden, eine Bijektion zwischen
den Hamiltonoperatoren und den reduzierten Einteilchendichten des
Grundzustandes besteht. Damit existiert ein exaktes Energiefunktional
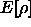 , nämlich das minimale
, nämlich das minimale 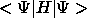 unter der
Nebenbedingung, daß
unter der
Nebenbedingung, daß 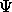 auf die gegebene Grundzustandsdichte
führt, also
auf die gegebene Grundzustandsdichte
führt, also 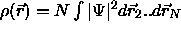 .
Das Variationsverfahren führt bei Beschränkung auf V-darstellbare
Dichten (solche, die Grundzustandsdichte eines Hamiltonoperators der
Form C.1 sein können) im Prinzip auf die richtige
Grundzustandsdichte. Die genaue funktionale Abhängigkeit von
.
Das Variationsverfahren führt bei Beschränkung auf V-darstellbare
Dichten (solche, die Grundzustandsdichte eines Hamiltonoperators der
Form C.1 sein können) im Prinzip auf die richtige
Grundzustandsdichte. Die genaue funktionale Abhängigkeit von 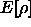 ist
bis heute nicht bekannt.
ist
bis heute nicht bekannt.