
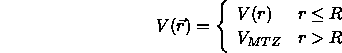
Die Schrödingergleichung läßt sich in Radial- und Winkelanteil separieren, und man erhält eine radiale Schrödingergleichung zu jeder Drehimpulsquantenzahl l. Uns interessieren nun die Partialwellen, das heißt die energieabhängigen Lösungen ohne Vorgabe von Randbedingungen.
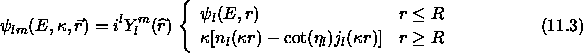
Wir normieren diese auf das Kugelvolumen
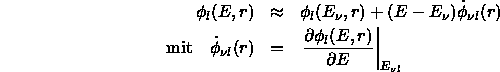
Wichtig sind nun die energieabhängigen Anschlußbedingungen der Funktion am Kugelrand, insbesondere das Verhalten der logarithmischen Ableitung und der (radial) logarithmische Ableitungen
Diese lassen sich durch vier Zahlen, sogenannte Potentialparameter, charakterisieren.
Soweit die Zustände in einer einzelnen Kugel. Sind nun Elektronenzustände in einem Kristall gesucht, dessen Elementarzelle in atomare muffin tin-Kugeln unterteilt ist, so sind jeweils die Anschlußbedingungen auf den Rändern dieser Kugeln zu erfüllen. Dazu addieren wir zur Partialwelle einen Term, der bei Überlagerung mit den Orbitalen der anderen Atome deren Ausläufer auslöschen soll. Auf diese Weise erhalten wir die muffin tin-Orbitale (MTO)
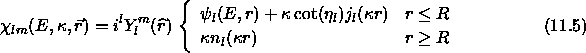
Die Ausläufer (auf englisch: tails) der MTO, die in alle anderen muffin tin-Kugeln hineinragen, lassen sich um die Zentren dieser Kugeln nach sphärischen Besselfunktionen entwickeln. Die Entwicklungskoeffizienten, die nur von der Anordnung und Größe der Kugeln, aber nicht vom Potential abhängen, heißen Strukturkonstanten.