



Next: Lokale Isomorphie und lokale
Up: Mathematische Grundbegriffe
Previous: Mathematische Grundbegriffe
Die Struktur von Festkörpern wird idealisiert als eine Menge von
Kernpositionen angegeben. Wie das Beispiel der Gläser zeigt, braucht
es sich bei Festkörpern weder um stabile Phasen noch um periodische
Strukturen zu handeln: Wir wollen nur fordern, daß die Strukturen
weder zu kleine Kernabstände (``hardcore condition'') noch
zu große Leerräume aufweisen sollen. Diese Voraussetzungen sind in
der mathematischen Begriffsbildung der
Delonemenge wiedergegeben:
Definition: (Delonemenge)
Eine Punktmenge 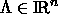 ist eine
Delonemenge genau dann, wenn folgende Bedingungen erfüllt sind:
ist eine
Delonemenge genau dann, wenn folgende Bedingungen erfüllt sind:
-
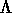 ist gleichmäßig diskret, d.h. es gibt einen
Minimalradius r , sodaß sich in jeder r-Kugel um einen
beliebigen Punkt aus
ist gleichmäßig diskret, d.h. es gibt einen
Minimalradius r , sodaß sich in jeder r-Kugel um einen
beliebigen Punkt aus 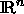 höchstens ein Punkt aus
höchstens ein Punkt aus 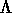 befindet.
befindet.
-
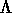 ist relativ dicht, d.h. es gibt einen
Maximalradius R, sodaß sich in jeder R-Kugel um einen beliebigen
Punkt aus
ist relativ dicht, d.h. es gibt einen
Maximalradius R, sodaß sich in jeder R-Kugel um einen beliebigen
Punkt aus 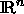 mindestens ein Punkt aus
mindestens ein Punkt aus 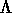 befindet.
befindet.
Eine Verallgemeinerung der periodischen Anordnung von
Elementarzellen stellen Tilings dar:
Definition(Tiling):
Ein Tiling ist eine Überdeckung
eines Raumes durch Mengen, die homöomorph zu Kugeln sind
(``Tiles''), ohne Lücken und Überlappungen, abgesehen von den
Rändern der Tiles, die eine Menge vom Maße 0 bilden sollen.
Die Tiles können als verallgemeinerte
Elementarzellen gelten, von denen es im Allgemeinen mehrere Sorten
(``Prototiles'') gibt und die nicht periodisch angeordnet sein
müssen. Als Beispiel für ein quasiperiodisches Tiling ist in
Abbildung 2 ein Ausschnitt aus dem zweidimensionalen
Tübinger Dreiecksmuster zu sehen, einem zehnzähligen Tiling
aus ``goldenen'' Dreiecken , das in [Baa90] beschrieben ist.
, das in [Baa90] beschrieben ist.
![]() ist eine
Delonemenge genau dann, wenn folgende Bedingungen erfüllt sind:
ist eine
Delonemenge genau dann, wenn folgende Bedingungen erfüllt sind:
 , das in [Baa90] beschrieben ist.
, das in [Baa90] beschrieben ist.