



Next: Beziehungen zwischen den Koordinatenräumen
Up: Streifenprojektionsmengen
Previous: Streifenprojektionsmengen
Wir wollen nun das
cut-and-project-Verfahren auf höhere Dimensionen verallgemeinern:
Seien 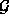 ein kubisches Gitter im
ein kubisches Gitter im 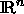 ,
, 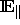 und
und
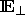 orthogonale Unterräume, die zusammen den
orthogonale Unterräume, die zusammen den 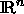 aufspannen, und
aufspannen, und
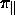 und
und 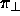 die Projektoren in diese Unterräume:
die Projektoren in diese Unterräume:
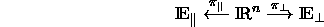
Die Unterräume seien derart gewählt, daß die Projektoren
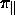 und
und 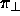 , eingeschränkt auf das Gitter
, eingeschränkt auf das Gitter 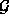 , bijektiv und die Bilder von
, bijektiv und die Bilder von 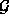 unter den Projektionen,
unter den Projektionen,
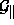 und
und 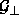 , dichte
, dichte
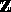 -Moduln sind.
-Moduln sind.

Im Falle eines primitiven Gitters 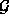 umfassen diese Moduln
genau die ganzzahligen Linearkombinationen der jeweiligen
Basisvektoren. Die
Moduln sind abzählbare Mengen und damit nicht vollständig. Sie sind
jedoch dichte Mengen in dem Sinne, daß jede
umfassen diese Moduln
genau die ganzzahligen Linearkombinationen der jeweiligen
Basisvektoren. Die
Moduln sind abzählbare Mengen und damit nicht vollständig. Sie sind
jedoch dichte Mengen in dem Sinne, daß jede  -Kugel um einen
Modulpunkt weitere Modulpunkte enthält. Da
-Kugel um einen
Modulpunkt weitere Modulpunkte enthält. Da 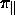 und
und
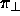 bei Einschränkung auf
bei Einschränkung auf 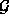 bijektiv sind, läßt
sich die Abbildung
bijektiv sind, läßt
sich die Abbildung 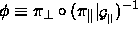 von
von 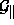 nach
nach 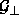 definieren. Die
Projektionen eines Gitterpunktes
definieren. Die
Projektionen eines Gitterpunktes 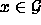 werden jeweils mit
werden jeweils mit
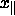 und
und 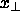 bezeichnet. Ich bezeichne die Komponenten
von x als die hochdimensionalen Koordinaten von x, die Komponenten
von
bezeichnet. Ich bezeichne die Komponenten
von x als die hochdimensionalen Koordinaten von x, die Komponenten
von 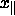 als die ``parallelen'' bzw. ``physikalischen'' und
die Komponenten von
als die ``parallelen'' bzw. ``physikalischen'' und
die Komponenten von 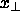 als die ``senkrechten'' bzw.
``internen'' Koordinaten.
als die ``senkrechten'' bzw.
``internen'' Koordinaten.
Zur Beschreibung von Quasigittern bzw. atomaren Strukturen soll nun
der Unterraum 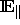 dienen. Die Punkte aus
dienen. Die Punkte aus 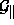 beschreiben mögliche Vertex- oder Atompositionen. Wir
lassen also keine allgemeinen Vektoren aus
beschreiben mögliche Vertex- oder Atompositionen. Wir
lassen also keine allgemeinen Vektoren aus 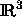 mehr als
Atomkoordinaten zu, allerdings läßt sich jeder reelle Vektor
beliebig gut durch Modulpunkte approximieren.
mehr als
Atomkoordinaten zu, allerdings läßt sich jeder reelle Vektor
beliebig gut durch Modulpunkte approximieren.
Um Delonemengen zu
erzeugen, müssen nun aus dem Modul 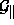 gewisse Punkte
ausgewählt werden. Zu diesem Zwecke verwendet man Mengen im
senkrechten Raum
gewisse Punkte
ausgewählt werden. Zu diesem Zwecke verwendet man Mengen im
senkrechten Raum 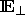 , sogenannte Fenster.
, sogenannte Fenster.
Definition (Fenster):
Eine Menge 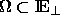 heißt Fenster genau dann, wenn
gilt:
heißt Fenster genau dann, wenn
gilt:
-
 ist kompakt und nicht leer.
ist kompakt und nicht leer.
-
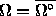
- Das Lebesguemaß des Randes
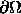 ist 0.
ist 0.
Definition (Streifenprojektionsmenge):
Sei 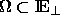 ein Fenster. Dann ist die mit
ein Fenster. Dann ist die mit  aus
aus  erzeugte Streifenprojektionsmenge (SPM) definiert
als
erzeugte Streifenprojektionsmenge (SPM) definiert
als
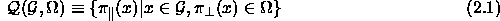
Diejenigen Modulpunkte, deren senkrechte Koordinaten im Fenster liegen,
bilden die SPM. Umgekehrt werden die in 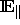 verstreuten Punkte der
SPM durch die Abbildung
verstreuten Punkte der
SPM durch die Abbildung 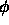 in eine kompakte Menge in
in eine kompakte Menge in
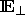 abgebildet. Gleichbedeutend mit
``SPM'' verwende ich auch die Bezeichnung Quasigitter.
abgebildet. Gleichbedeutend mit
``SPM'' verwende ich auch die Bezeichnung Quasigitter.
Die Punkte mit 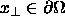 heißen singulär, bilden
eine Menge vom Maße 0 und werden im folgenden vernachlässigt.
heißen singulär, bilden
eine Menge vom Maße 0 und werden im folgenden vernachlässigt.
Die Dualisierungsmethode, ein analoges Verfahren zur Erzeugung
quasiperiodischer Tilings ist in Anhang
A geschildert. Die Vertizes eines derart erzeugten
Tilings bilden wiederum ein Quasigitter.




Next: Beziehungen zwischen den Koordinatenräumen
Up: Streifenprojektionsmengen
Previous: Streifenprojektionsmengen