Eine globale Translation eines Kristallgitters wirkt sich im
Beugungsbild lediglich durch globale und in gewöhnlichen
Beugungsmethoden ``unsichtbare'' Phasenfaktoren aus,
genauer gesagt, durch drei unabhängige Phasen für die drei Raumrichtungen.
In Analogie dazu können wir bei den ikosaedrischen Quasikristallen
sechs Phasenfaktoren frei wählen. Diese sechs Freiheitsgrade
entsprechen im Bilde der Schnittmethode der Wahl eines
sechsdimensionalen Aufpunktes für den Schnitt, also drei
physikalischen und drei internen, sogenannten phasonischen
Freiheitsgraden. Verschiebt man den Schnitt um einen reellen Vektor
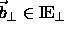, so werden in 
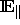an manchen Stellen Punkte
verschwinden, an anderen neue Punkte auftauchen. Die closeness
condition ist die Forderung an die Wahl der Fenster, daß das
Verschwinden und Auftauchen von Punkten immer gleichzeitig an
benachbarten Stellen geschehen soll, sodaß beim Verschieben des
Schnittes lediglich Sprünge im physikalischen Raum, sogenannte
Flips, auftreten. Die Flips sind über weite Strecken miteinander
korreliert (siehe Abbildung 2), und
das durch die Verschiebung entstehende Tiling ist lokal isomorph zum
ursprünglichen.
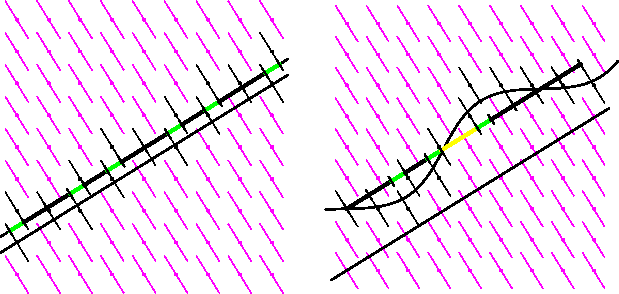
Abbildung 2.4: Verschiebung des Schnittes und lokale Phasonen
In Analogie zu den Phononen, ortsabhängigen Translationen eines
Gitters, kann man eine ortsabhängige Verbiegung des Schnittraumes einführen,
die zu lokalen, unkorrelierten Flips, sogenannten Phasonenstörungen
führt. (siehe Abbildung 2).
Durch die Durchführung von Phasonenflips lassen sich aus einem
idealen Tiling Random Tilings gewinnen.
Diese sind nicht mehr lokal isomorph zu idealen Tilings. Im
Beugungsbild machen sich beschränkte Fluktuationen des Schnittes
durch einen Debye-Waller-Faktor für die Reflexe und durch
diffuse Streuung bemerkbar.
Entfernt sich dagegen der Schnitt mit zunehmendem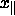 
im Mittel
linear vom ursprünglichen Schnitt, so verschieben sich die Braggreflexe,
und die Symmetrie des Beugungsbildes ändert sich. Im Falle eines
geraden Schnittes mit rationaler Steigung erhält man als Resultat der
phasonischen Störungen einen periodischen Approximanten, dessen
Beugungsbild ein gewöhnliches Gitter ist. Wird der Schnitt derart gewählt,
daß 
durch einen genäherten Wert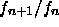 
mit
aufeinanderfolgenden Fibonaccizahlen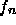 
und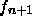 
ersetzt wird,
spricht
man von einem 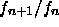-Approximanten. Mit besserer Annäherung von
durch höhere Fibonaccizahlen wächst die Größe des
Approximanten und bildet eine immer bessere Annäherung an die ideale
Struktur. Durch die Einführung der
Phasonen kommt man zur Betrachtung eines statistischen Ensembles von
Random Tilings. Die vielen Realisierungsmöglichkeiten führen zu
einem Entropiebeitrag. In den Random Tiling Modellen wird angenommen,
daß dies der entscheidende Beitrag zur freien Energie F=U-TS ist,
der zu einer Stabilisierung der quasikristallinen Phase führt. Diese
Annahme wird durch die Tatsache gestützt, daß alle
bisher bekannten Quasikristalle Hochtemperaturphasen sind.