Die Zellparameter aller mit LMTO untersuchten Strukturen sind in Tabelle D.3 zusammengestellt. Sie enthält von links nach rechts: exakte Stöchiometrie, Stöchiometrie in Prozent, Raumgruppe, Atome/Zelle, Klassen inäquivalenter Atome, Netz von
Die Geometrie der freien Cluster wurde für die Rechnungen mit
gaussian94 in Form der Z-Matrix definiert, die für jedes Atom
Abstände und Winkel bezüglich bereits definierter Atome enthält.
Die genaue Definition findet sich im gaussian-Handbuch. Die Z-Matrix
für den Bergmancluster (Cu, Dummy-Atom X, Al mit Zentralabständen
![]() 0.27605 nm und
0.27605 nm und ![]() 4.065 nm)
ist in Tabelle D.2 dargestellt.
4.065 nm)
ist in Tabelle D.2 dargestellt.
Die Zellparameter aller mit LMTO untersuchten Strukturen sind in Tabelle
D.3 zusammengestellt. Sie enthält von links
nach rechts: exakte Stöchiometrie, Stöchiometrie in Prozent,
Raumgruppe, Atome/Zelle, Klassen inäquivalenter Atome, Netz von
![]() -Punkten in der Brillouin-Zone zur selbstkonsistenten Rechnung,
Anzahl irreduzibler
-Punkten in der Brillouin-Zone zur selbstkonsistenten Rechnung,
Anzahl irreduzibler ![]() -Punkte.
-Punkte.
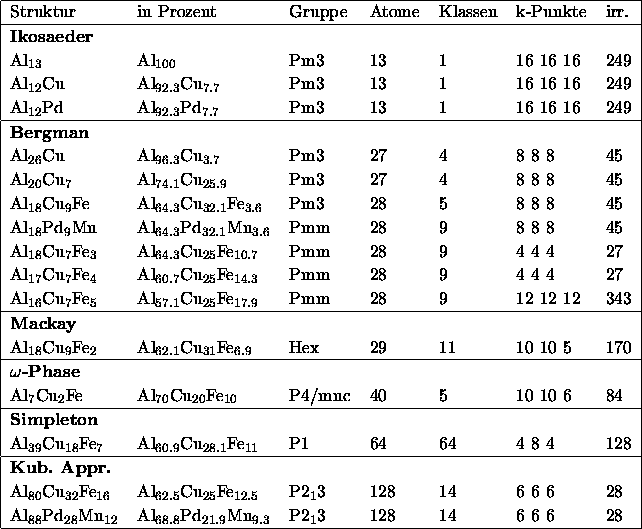
Tabelle D.3: Modellstrukturen der LMTO-Rechnungen
Die Koordinaten finden sich in den folgenden Tabellen:
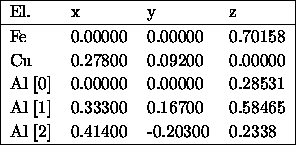
Ikosaeder und Bergmancluster
Die Zelle ist kubisch mit Gitterkonstanter ![]() ,
also 0.7597 nm für AlCuFe und 0.7760 nm für AlPdMn entsprechend
den Größen im Quasikristall. Die Tabelle enthält die Koordinaten in
Einheiten der Gitterkonstanten, wobei der Cluster in der Zellmitte
zentriert ist. Für die verschiedenen Stöchiometrien
(in der Reihenfolge von Tabelle D.3) ist die
Verteilung der Elemente angegeben.
,
also 0.7597 nm für AlCuFe und 0.7760 nm für AlPdMn entsprechend
den Größen im Quasikristall. Die Tabelle enthält die Koordinaten in
Einheiten der Gitterkonstanten, wobei der Cluster in der Zellmitte
zentriert ist. Für die verschiedenen Stöchiometrien
(in der Reihenfolge von Tabelle D.3) ist die
Verteilung der Elemente angegeben.

Mackaycluster
Gleiche Zelle wie zuvor, der Cluster ist in der Zellecke zentriert.

Al![]() Cu
Cu![]() Fe
Fe
Tetragonal mit a=0.6336 nm und c=1.4870 nm
(siehe Structure reports 13, S.9).
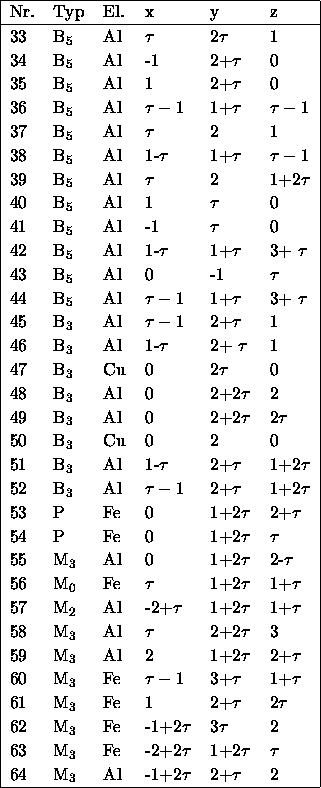
Kubische Approximanten
Die Koordinaten für Al![]() Cu
Cu![]() Fe
Fe![]() sind in [Cock93]
veröffentlicht. Eine Analyse der Geometrie ergibt eine Zuordnung
zu Punkttypen, und mit Elsers Dekorationsvorschlag
folgt in der Numerierung von Cockayne:
sind in [Cock93]
veröffentlicht. Eine Analyse der Geometrie ergibt eine Zuordnung
zu Punkttypen, und mit Elsers Dekorationsvorschlag
folgt in der Numerierung von Cockayne:

Simpletonzelle
Gittervektoren ![]() ,
, ![]() und
und ![]() .
.
Die Koordinaten erhalten noch den Vorfaktor
![]() 0.8383 nm.
0.8383 nm.