Die Fenster für Punktcluster auf ikosaedrischen Tilings

In einfachen Modellen für Quasikristalle nimmt man an, daß die Atome sich auf den Vertizes eines Tilings befinden. In den folgenden Kapiteln wird ein Modell behandelt, in dem Cluster von Atomen ein 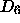-Gitter, also die Vertizes eines 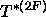-Tilings besetzen. Ausgehend vom Fenster für die Vertizes und der Gestalt des Clusters soll das Fenster für die Atompositionen bestimmt werden. Dazu dient folgender Satz:
Falls 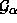eines der 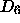-Gitt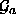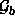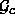er , , oder 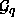ist und 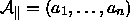eine Menge von Parallelraumvektoren, die der Klasse 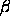angehören, so gilt:

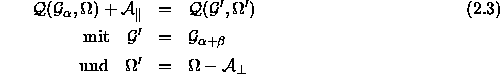
Wird also jeder Punkt eines Quasigitters durch eine Menge von Punkten ersetzt, so ergibt sich das Fenster des neuen Quasigitters als Vereinigung verschobener Kopien des ursprünglichen Fensters. In Kapitel 5 werden wir ikosaedersymmetrische Clusterschalen betrachten. Die Angabe eines einzigen repräsentativen Verschiebungsvektors (Zentralatom-Clusteratom) genügt dabei, um das Fenster des entstehenden Quasigitters zu charakterisieren.