Die Ikosaedergruppe I ist die Drehgruppe des platonischen Ikosaeders.
Sie wird erzeugt durch Generatoren 
und 
mit den Eigenschaften
Dies sind Drehungen um eine zweizählige und um eine benachbarte
fünfzahlige Achse. I umfaßt 60 Gruppenlemente und besitzt
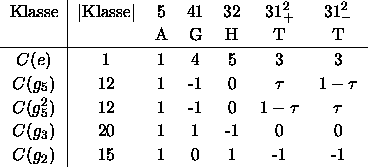
Untergruppen der Ordnungen 2, 3 und 5. Die Charaktere 
der
Ikosaedergruppe sind in der folgenden Tafel
gezeigt:
Läßt man noch die Rauminversion i mit 
zu, gelangt man zur
Punktgruppe des Ikosaeders. Sie enthält Spiegelebenen und
umfaßt insgesamt 120 Gruppenelemente. Bei den Darstellungen bezeichnen
g und u gerades bzw. ungerades Verhalten bei Rauminversion.
Die Ikosaedergruppe läßt sich als Permutationsgruppe der
Ikosaederecken auffassen. Nach der Wahl von sechs Ikosaederecken 
wie in 2
lassen sich die Gruppenelemente als Permutationen mit Vorzeichenwechsel
schreiben:
Damit ist die Gruppe in die sechsdimensionale hyperkubische Gruppe
eingebettet.
Schreibt man die Gruppenelemente in Form sechsdimensionaler Matrizen, so
zerfällt der 
in zwei dreidimensionale invariante Unterräume
und 
zu den beiden dreidimensionalen Darstellungen von I.