Wenn der Zwischenraum zwischen den Kugeln relativ klein ist, kann eine
weitere Vereinfachung getroffen werden: die
Beziehung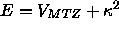 
wird ignoriert und stattdessen für die
Ausläufer der MTO mit einem festen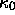 
gearbeitet. Durch diese
Näherung, die atomic sphere approximation (ASA) und durch die
Verwendung modifizierter Bessel- und Neumannfunktionen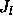 
bzw.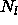 
erhalten wir
energieunabhängige augmentierte MTO
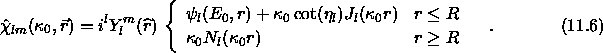
Sie sind stetig, differenzierbar, orthogonal zu den Corezuständen und
damit geeignete Basiszustände. Als Basis werden für jeden
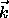-Vektor Blochsummen aus energieunabhängigen MTO verwendet,
und das Variationsproblem reduziert sich auf die Diagonalisierung der
LMTO-Säkularmatrix (siehe [Skriver], Kapitel 5). Dabei gehen
die Anschlußbedingungen zwischen den Kugeln in Form der
Potentialparameter und Strukturkonstanten in die Rechnung ein.
Das Volumen der Zwischenräume und das Volumen von Kugelüberlappungen
gehen quadratisch in den Fehler der ASA ein: Deshalb werden in die
Zelle atomare Kugeln derart einbeschrieben, daß die Summe der
Kugelvolumina gerade das Zellvolumen ergibt (``Wigner-Seitz-Kugeln''),
und gegebenenfalls werden Leerkugeln mit eigenen Orbitalen in den
Lücken zwischen den Atomen eingeführt. Der verbleibende Fehler wird
durch die combined correction (siehe [Skriver], Abschnitt
6.9) teilweise korrigiert.