



Next: Elektronen in isolierten Metallclustern
Up: Die Fenster zum Elsermodell
Previous: Der Vergleich mit anderen
Mit Hilfe der Fenster lassen sich in Elsers Modell Schalenstrukturen
um Bergmancluster und Mackaycluster finden, das heißt,
ikosaedersymmetrische Punktmengen, die ganz oder teilweise mit Atomen
besetzt sind. Die Schalen können große Zwischenräume aufweisen, in
denen viele weitere Atome unsymmetrisch angeordnet sind.
Sie lassen
sich folgendermaßen nachweisen: eine Schale, charakterisiert durch
die Klasse des Zentralatoms sowie einen Verschiebungsvektor
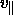 , wird gesucht. Als Verschiebungvektoren kommen die
Standardvektoren
, wird gesucht. Als Verschiebungvektoren kommen die
Standardvektoren 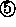 ,
, 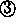 und
und 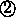 mit
mit  -Potenzen als
Vorfaktoren in Frage. Wenn das Fenster der Schalenatome eine
Untermenge des Elserfensters zur entsprechenden Punktklasse ist, so
ist die Schale um jedes entsprechende Zentralatom vollständig
vorhanden. Neben der
-Potenzen als
Vorfaktoren in Frage. Wenn das Fenster der Schalenatome eine
Untermenge des Elserfensters zur entsprechenden Punktklasse ist, so
ist die Schale um jedes entsprechende Zentralatom vollständig
vorhanden. Neben der 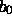 -Punkten (Klasse a) und den
-Punkten (Klasse a) und den 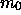 -Punkten
(Klasse q) kann man auch diejenigen Punkte der anderen Klassen b
und c betrachten, die durch das Triakontaeder codiert werden. Wir
suchen Schalen um all diese Punktsorten. Ein verschobenes
Testtriakontaeder muß also in das in Frage kommende Fenster
hineinpassen. Mögliche
-Punkten
(Klasse q) kann man auch diejenigen Punkte der anderen Klassen b
und c betrachten, die durch das Triakontaeder codiert werden. Wir
suchen Schalen um all diese Punktsorten. Ein verschobenes
Testtriakontaeder muß also in das in Frage kommende Fenster
hineinpassen. Mögliche 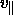 sind in der Tabelle
5.3 aufgeführt, zusammen mit Angaben über das
Auftreten von Schalen dieser Größe um Mittelpunkte der verschiedenen
Klassen. Geordnet nach Klassen der Schalenatome ergeben sich folgende
Fälle:
sind in der Tabelle
5.3 aufgeführt, zusammen mit Angaben über das
Auftreten von Schalen dieser Größe um Mittelpunkte der verschiedenen
Klassen. Geordnet nach Klassen der Schalenatome ergeben sich folgende
Fälle:
- Klasse a: Mit wachsendem
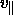 geht
geht 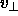 gegen 0,
bleibt aber endlich. Da das a-Fenster selber nur ein Triakontader
ist, liegt das Testtriakontaeder nie vollständig im Fenster. Die
Schalen werden umso vollständiger, je größer sie gewählt sind,
bleiben aber immer unvollständig.
gegen 0,
bleibt aber endlich. Da das a-Fenster selber nur ein Triakontader
ist, liegt das Testtriakontaeder nie vollständig im Fenster. Die
Schalen werden umso vollständiger, je größer sie gewählt sind,
bleiben aber immer unvollständig.
- Klasse b: In fünfzähliger Richtung liegt das Triakontaeder bei einer
Verschiebung um
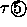 oder kleiner vollständig im Fenster, in
dreizähliger bei
oder kleiner vollständig im Fenster, in
dreizähliger bei 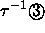 oder kleiner,
bei zweizähliger in
oder kleiner,
bei zweizähliger in 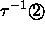 oder kleiner.
Das entspricht im Parallelraum Zentralabständen von
oder kleiner.
Das entspricht im Parallelraum Zentralabständen von
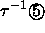 ,
, 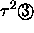 ,
, 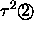 oder
jeweils größeren.
oder
jeweils größeren.
- Klasse c: Keine Punkte vorhanden
- Klasse q: In fünfzähliger Richtung liegt das Triakontaeder bei einer
Verschiebung um
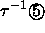 oder kleiner vollständig im Fenster, in
dreizähliger bei
oder kleiner vollständig im Fenster, in
dreizähliger bei 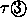 oder kleiner,
bei zweizähliger in
oder kleiner,
bei zweizähliger in 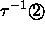 oder kleiner. Das entspricht im
Parallelraum Zentralabständen von
oder kleiner. Das entspricht im
Parallelraum Zentralabständen von 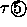 ,
, 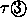 ,
, 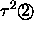 oder
jeweils größeren.
oder
jeweils größeren.
Die folgende Tabelle zeigt in den letzten vier Spalten noch einmal die
Schalen geordnet nach den Klassen der Mittelpunkte. Neben der Klasse
der Schalenatome ist jeweils der Grad der Vollständigkeit
aufgeführt: ``v'' bedeutet, daß um all diese Zentren vollständige
Schalen zum Verschiebungsvektor 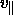 vorliegen, ``t''
bedeutet, daß teilweise gefüllte Schalen vorliegen. Wir finden
natürlich die bekannten
Schalen der Bergman- und Mackaycluster um a- und q-Punkte.
vorliegen, ``t''
bedeutet, daß teilweise gefüllte Schalen vorliegen. Wir finden
natürlich die bekannten
Schalen der Bergman- und Mackaycluster um a- und q-Punkte.
Man beachte nun die ungefähre Symmetrie zwischen den Klassen b und
q beziehungsweise a und c im Hinblick auf die Größe der
Fenster: es bilden sich eine zweite Sorte von ``b''-Mackayclustern
um b-Punkte und eine zweite Sorte von ``c''-Bergmanclustern um
c-Punkte. Beide Sorten von Clustern sind unvollständig. Die
b-Mackaycluster wurden in Abschnitt 3
bereits erwähnt, die c-Bergmancluster finden sich im PR zwischen
den drei benachbarten a-Bergmanclustern in der in Abbildung
5.10 gezeigten Konfiguration. Die vorletzte und
letzte Spalte der Tabelle enthalten die entsprechenden Clusterschalen.
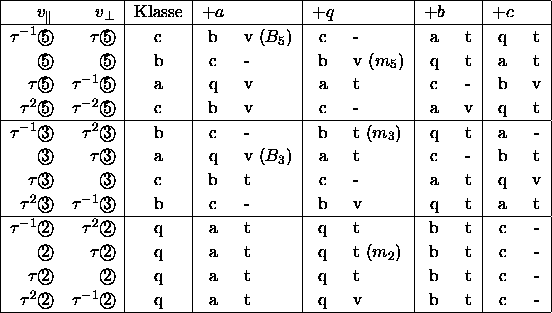
Tabelle: Höhere Clusterschalen
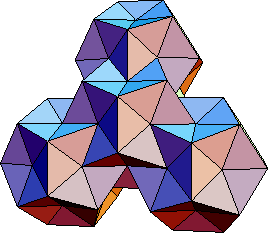
Abbildung: Der unvollständige Bergmancluster um c-Punkte




Next: Elektronen in isolierten Metallclustern
Up: Die Fenster zum Elsermodell
Previous: Der Vergleich mit anderen

