Die Fenster aus 5
lassen sich gut mit experimentell bestimmten Fenstern
der französischen Gruppen Katz, Gratias et al. und Boudard, die
Boissieu et al. vergleichen. Dies ist natürlich äquivalent zu einem
Vergleich der Modelle im physikalischen Raum. Eine Schwierigkeit ist
beim Vergleich zu beachten: die Zuordnung der Fenster zu den Punktklassen
hängt von der Wahl der Basis ab, die ein bestimmtes
Skalierungsverhalten nach sich zieht, und außerdem von der Wahl des
Gitternullpunktes. Ich ordne die Fenster der anderen Gruppen den
Klassen so zu, wie es der hier verwendeten Konvention entspricht. In
diesem Abschnitt ist wiederum nur von den geometrischen
Strukturen die Rede, die chemische Ordnung in den Modellen
ist in Anhang B besprochen.
Katz und Gratias machen für ihr Modell folgende Annahmen: Die Fenster
sind ikosaedersymmetrische Polytope mit homogener Punktdichte, und sie
sollen die hardcore und die closeness condition erfüllen. Damit
müssen sie von zweizähligen Flächen begrenzt sein. In [Katz92]
werden für i-AlCuFe folgende Fenster vorgeschlagen (siehe Abbildung
5.8):
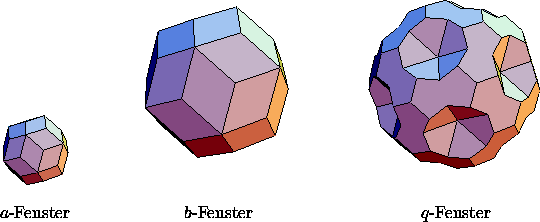
Abbildung: Die Fenster von Katz und Gratias für c-, b- und q-Punkte
Katz und Gratias berichten für dieses Modell eine gute Wiedergabe
ihrer Beugungsdaten. Die Fenster für Elsers Modell, wie in Abschnitt
5 dargestellt, weisen eine große Ähnlichkeit mit
denen von Katz und Gratias auf. Aus den Unterschieden der Fenster
folgen die Unterschiede der Modelle im physikalischen Raum: bei Katz
und Gratias ist die Auswahl der ![]() - und
- und ![]() -Punkte durch die
Fenster festgelegt, sie sind also über große Entfernungen streng
korreliert. Außerdem kommt es vor, daß die Wahl der
-Punkte durch die
Fenster festgelegt, sie sind also über große Entfernungen streng
korreliert. Außerdem kommt es vor, daß die Wahl der ![]() -Positionen
beide möglichen Positionen für ein
-Positionen
beide möglichen Positionen für ein ![]() -Atom ausschließt. Dies
führt zu einer
etwas verminderten Dichte.
-Atom ausschließt. Dies
führt zu einer
etwas verminderten Dichte.
Boudard und de Boissieu [Bou92], [Boi94] haben an ihre
Beugungsdaten für i-AlPdMn, kugelförmige Fenster angepaßt, die in
erster Linie das Volumen der tatsächlichen Fenster wiedergeben
sollen, dabei aber die hardcore condition verletzen. Ebenso wie im
Modell von Katz und Gratias ist hier nicht an Unordnung im Sinne eines
Random Tilings gedacht. Ein Vergleich der Volumina in Einheiten von
30K ergibt eine relativ gute Übereinstimmung zwischen den drei
Modellen:

Elsers Modell ergibt eine Dichte von ca. 69.12 Atomen/nm![]() für AlCuFe und
64.85 Atomen/nm
für AlCuFe und
64.85 Atomen/nm![]() für AlPdMn. Zum Vergleich: Aluminium in fcc-Struktur mit
Gitterkonstante 0.404 nm enthält ca. 60.66 Atome/nm
für AlPdMn. Zum Vergleich: Aluminium in fcc-Struktur mit
Gitterkonstante 0.404 nm enthält ca. 60.66 Atome/nm![]() .
.
Das Modell von C. Janot [Jan97] für i-AlPdMn beruht auf der einer Anordnung atomarer Mackaycluster auf einer selbstähnlichen hierarchischen Punktmenge: Die Cluster sind - als ``vergrößerte Atome'' - wiederum zu Mackaylustern angeordnet, die ihrerseits wieder größere Mackaycluster bilden und so fort. Beginnt man bei der iterativen Erzeugung der Mackayzentren mit einem Mackayzentrum der Klasse q, so sind nach zwei Iterationsstufen alle vier Klassen q, a, b und c bevölkert, und zwar mit den Anzahlen 3357, 276, 1304 und 1284.
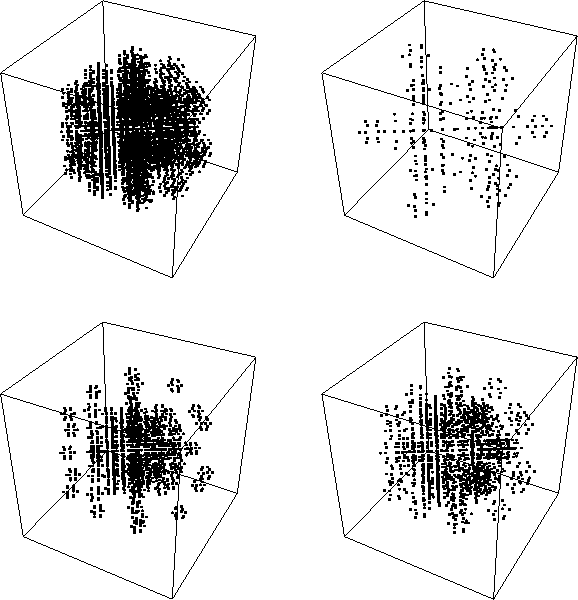
Abbildung 5.9: Janots Modell: Zentren der atomaren Mackaycluster nach der zweiten
Inflation im internen Raum, Klassen q, a, b und c.
Abbildung 5.9 zeigt die Punktwolken im internen Raum. Nach Elsers Modell - das in diesem Punkt im Einklang mit den Beugungsdaten steht - dürften hier ausschließlich die Punktklassen q und b bevölkert sein. Hält der Trend zur gleichmäßigen Verteilung der Atome über die Punktklassen für höhere Inflationsstufen an, so unterscheidet sich Janots Modell damit erheblich von den bisher genannten.