 entwickelt, so reduziert sich
das Variationsproblem
entwickelt, so reduziert sich
das Variationsproblem mit Hamiltonmatrix
Die DOS n(E) läßt sich formal umschreiben:
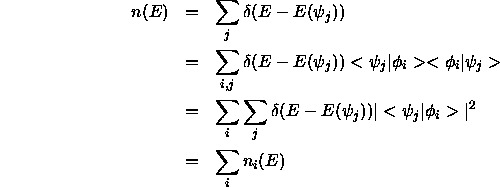
und als Summe von sogenannten projizierten Zustandsdichten (PDOS)
Bei einer Basis aus ebenen Wellen
Werden die Zustände nach einem endlichen Satz von Basisfunktionen ![]()
 entwickelt, so reduziert sich
das Variationsproblem
entwickelt, so reduziert sich
das Variationsproblem ![]() auf ein
Eigenwertproblem für die Entwicklungskoeffizienten
auf ein
Eigenwertproblem für die Entwicklungskoeffizienten ![]() :
:
![]()
mit Hamiltonmatrix ![]() und Überlappmatrix
und Überlappmatrix ![]() .
Als Basissätze werden beispielsweise die aus ebenen Wellen
.
Als Basissätze werden beispielsweise die aus ebenen Wellen
![]() durch
Orthogonalisierung auf die Corezustände erzeugten
orthogonalisierten ebene Wellen verwendet. Als lokalisierte
Basisfunktionen eignen sich die feste Linearkombinationen sogenannter
Gauss-type orbitals:
durch
Orthogonalisierung auf die Corezustände erzeugten
orthogonalisierten ebene Wellen verwendet. Als lokalisierte
Basisfunktionen eignen sich die feste Linearkombinationen sogenannter
Gauss-type orbitals:
![]() .
Da
man mit der Basis die möglichen Lösungen auf einen Unterraum des
Hilbertraums einschränkt, ist man bestrebt, die Basis so raffiniert
zu wählen, daß man bereits mit wenigen Basisfunktionen eine gute
Näherung der tatsächlichen Lösung erhält. Dies ist aber auch der
Hauptnachteil des Verfahrens: für eine realistische Beschreibung
benötigt man eventuell einen großen Basissatz oder muß für schwere
Atome mit Pseudopotentialen
arbeiten.
.
Da
man mit der Basis die möglichen Lösungen auf einen Unterraum des
Hilbertraums einschränkt, ist man bestrebt, die Basis so raffiniert
zu wählen, daß man bereits mit wenigen Basisfunktionen eine gute
Näherung der tatsächlichen Lösung erhält. Dies ist aber auch der
Hauptnachteil des Verfahrens: für eine realistische Beschreibung
benötigt man eventuell einen großen Basissatz oder muß für schwere
Atome mit Pseudopotentialen
arbeiten.
Die DOS n(E) läßt sich formal umschreiben:
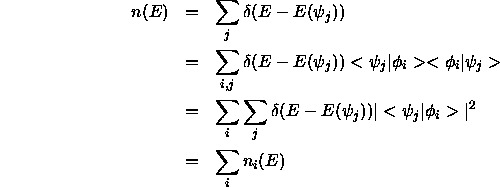
und als Summe von sogenannten projizierten Zustandsdichten (PDOS)
![]() auffassen. Bei einer lokalen Basis erhalt man die Beiträge
einzelner Orbitale, Atome oder Atomsorten zur gesamten DOS. Diese
sind in erster Linie nur von den lokalen Umgebungen der
jeweiligen Orbitale abhängig, was bei Verwendung einer
Tight-Binding-Basis aus dem Momentetheorem (Abschnitt
6) folgt. So läßt sich die DOS in der
Blickweise der Chemie als Ausdruck lokaler Bindungen deuten, die in
den jeweiligen PDOS
zur Aufspalten, Anheben oder Absenken von Zuständen führen.
auffassen. Bei einer lokalen Basis erhalt man die Beiträge
einzelner Orbitale, Atome oder Atomsorten zur gesamten DOS. Diese
sind in erster Linie nur von den lokalen Umgebungen der
jeweiligen Orbitale abhängig, was bei Verwendung einer
Tight-Binding-Basis aus dem Momentetheorem (Abschnitt
6) folgt. So läßt sich die DOS in der
Blickweise der Chemie als Ausdruck lokaler Bindungen deuten, die in
den jeweiligen PDOS
zur Aufspalten, Anheben oder Absenken von Zuständen führen.
Bei einer Basis aus ebenen Wellen ![]() erhält man als PDOS für jeweils ein
erhält man als PDOS für jeweils ein ![]() die
Spektralfunktion
die
Spektralfunktion ![]()