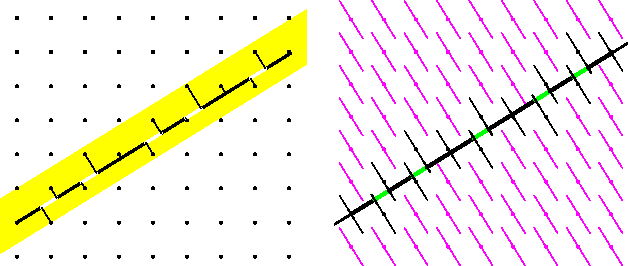
Abbildung 2.3: Streifen- und Schnittkonstruktion der Fibonaccikette
Um die Fibonaccikette weiter zu untersuchen, bedient man sich einer
weiteren, völlig anderen Konstruktion, des
cut-and-project-Verfahrens (siehe Abbildung 2):

Abbildung 2.3: Streifen- und Schnittkonstruktion der Fibonaccikette
Sei ![]() das Quadratgitter im
das Quadratgitter im ![]() . Wir
betrachten nun eine Zerlegung des
. Wir
betrachten nun eine Zerlegung des ![]() in zwei orthogonale
Unterräume (Geraden)
in zwei orthogonale
Unterräume (Geraden) ![]() und
und ![]() :
: ![]() sei die Gerade durch den
Ursprung mit der Steigung
sei die Gerade durch den
Ursprung mit der Steigung ![]() . Die Zahl
. Die Zahl
![]() , der goldene Schnitt, ist im Anhang
A näher beschrieben. Die Projektoren auf die Unterräume
heißen
, der goldene Schnitt, ist im Anhang
A näher beschrieben. Die Projektoren auf die Unterräume
heißen ![]() und
und ![]() und bilden das Gitter
und bilden das Gitter
![]() auf die
auf die ![]() -Moduln
-Moduln ![]() und
und
![]() ab. Die Elemente der Moduln sind vom Typ
ab. Die Elemente der Moduln sind vom Typ
![]() in
in ![]() und
und ![]() .
Da die Steigung von
.
Da die Steigung von ![]() eine irrationale Zahl
ist, ist die Abbildung
eine irrationale Zahl
ist, ist die Abbildung ![]() , eingeschränkt auf die
Gitterpunkte, eine Bijektion. Dasselbe gilt für
, eingeschränkt auf die
Gitterpunkte, eine Bijektion. Dasselbe gilt für ![]() , und
damit läßt sich jedem Punkt
, und
damit läßt sich jedem Punkt ![]() , der zum Modul
, der zum Modul
![]() gehört - und nur solche werden im folgenden
betrachtet - eine ``senkrechte'' Koordinate
gehört - und nur solche werden im folgenden
betrachtet - eine ``senkrechte'' Koordinate ![]() zuordnen. Diese Abbildung
zuordnen. Diese Abbildung ![]() zwischen
zwischen
![]() und
und
![]() ist linear, aber überall unstetig.
ist linear, aber überall unstetig.
Wir wollen nun eine Delonemenge erzeugen: Dazu wählen wir einen
Streifen der Breite ![]() und projiziert
nur die Punkte, die innerhalb des Streifens liegen.
und projiziert
nur die Punkte, die innerhalb des Streifens liegen.
In der alternativen sogenannten Schnittkonstruktion werden atomare
Hyperflächen an den Punkten des Gitters befestigt, und die
Struktur entsteht durch Schnitt des Raumes ![]() mit den
Hyperflächen. (Siehe Abbildung 2). Wenn die atomaren
Hyperflächen identisch mit dem gespiegelten Streifendurchmesser sind,
sind diese beiden Konstruktionen
äquivalent.
mit den
Hyperflächen. (Siehe Abbildung 2). Wenn die atomaren
Hyperflächen identisch mit dem gespiegelten Streifendurchmesser sind,
sind diese beiden Konstruktionen
äquivalent.
Die resultierende Punktmenge, ein einfaches Beispiel und gleichzeitig
das Paradigma einer Streifenprojektionsmenge, hat
tatsächlich die Deloneeigenschaft und weist zwei verschieden lange
Abstände - im Verhältnis 1 zu
![]() - auf, die nach dem Schema der Fibonaccikette angeordnet sind.
- auf, die nach dem Schema der Fibonaccikette angeordnet sind.
Festzuhalten ist: die quasiperiodische Fibonaccikette ist durch
Projektion eines periodischen Gitters höherer Dimension
konstruiert worden. Die zusätzliche interne Dimension
beherbergt das Fenster - in diesem Fall einfach die
Streifenbreite - das bestimmt, welche Punkte für die Projektion
freigegeben sind. Ein äquivalente Konstruktionsmethode derselben
Struktur besteht im Schnitt durch eine
Menge von gespiegelten Fenstern, die an den
hochdimensionalen Gitterpunkten zentriert sind.