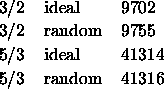
Es stehen Datensätze für ideale und randomisierte kubische 3/2- und
5/3-Approximanten zur Verfügung. Die Anzahlen der
Vertizes betragen 576 bzw. 2440, die Kantenlängen der Zellen
betragen ![]() (
(![]() 5.207 nm für AlCuFe) beziehungsweise
5.207 nm für AlCuFe) beziehungsweise
![]() (
(![]() 8.425 nm für AlCuFe).
Die Anzahl der Atome beträgt für die
verschiedenen Approximanten:
8.425 nm für AlCuFe).
Die Anzahl der Atome beträgt für die
verschiedenen Approximanten:

Abbildung 4.1: Der randomisierte 3/2-Approximant
Abbildung 4.1 zeigt die Einheitszelle des
randomisierten 3/2-Approximanten, aus einer fünfzähligen Richtung
gesehen. Viele Atome sind durch andere verdeckt. Die durchlaufenden
Ebenen hoher Atomdichte sind als Linien sichtbar. Ein Bergmancluster
ist am rechten oberen Rand des Clusters gut zu erkennen: das
![]() -Atom ist von zwei konzentrischen Zehnecken, den
-Atom ist von zwei konzentrischen Zehnecken, den ![]() - und
- und
![]() -Atomen umgeben.
-Atomen umgeben.
Verschiedene Größen lassen sich mit den bekannten Werten der unendlich ausgedehnten Quasiperiodischen Struktur vergleichen:
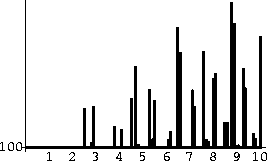
Abbildung: Häufigkeiten atomarer Abstände in Angström im idealen kubischen
3/2-Approximanten
 recht gut, wie
das Beispiel des idealen 5/3 Approximanten in der folgenden
Tabelle zeigt: die Häufigkeiten der Atomsorten sind hier auf die
Häufigkeit der a-Vertizes normiert.
recht gut, wie
das Beispiel des idealen 5/3 Approximanten in der folgenden
Tabelle zeigt: die Häufigkeiten der Atomsorten sind hier auf die
Häufigkeit der a-Vertizes normiert.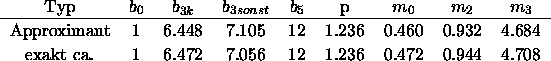
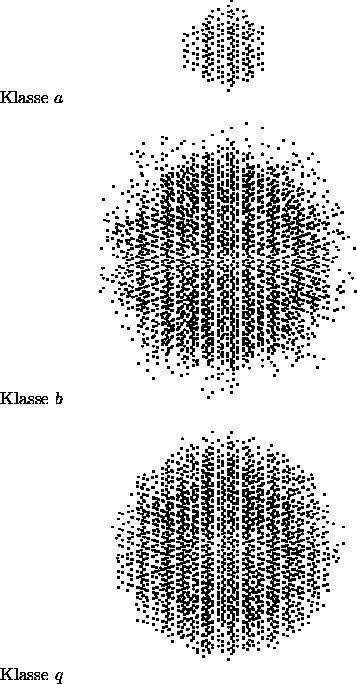
Abbildung: Interne Koordinaten für den idealen 3/2-Approximanten
In Abbildung 4.4 sind für die 5/3-Approximanten die spärisch gemittelten Punktdichten im internen Raum in Abhängigkeit vom Betrag der internen Koordinate (in nm) gezeigt. Wie zu erwarten, verlagern sich durch die Randomisierung die Punkte nach außen.
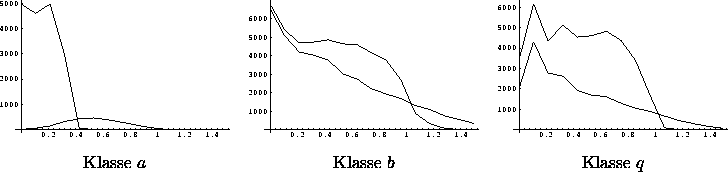
Abbildung: Punktdichten im internen Raum für den idealen und den
randomisierten 5/3-Approximanten