Genauso verfährt man bei der Konstruktion für die restlichen Punkttypen:
Die Fenster der Zentalatome ![]() bzw.
bzw. ![]() sind um
sind um ![]() skalierte kanonische Triakontaeder.
Bekannt sein müssen jeweils die Klasse des jeweiligen Zentralatoms
(a für Bergman, q für Mackay), und der Abstandsvektor
skalierte kanonische Triakontaeder.
Bekannt sein müssen jeweils die Klasse des jeweiligen Zentralatoms
(a für Bergman, q für Mackay), und der Abstandsvektor
![]() von Zentrum zu den Schalenpunkten.
von Zentrum zu den Schalenpunkten.
 und sind in Tabelle 5.1
in Einheiten von
30K mit
und sind in Tabelle 5.1
in Einheiten von
30K mit
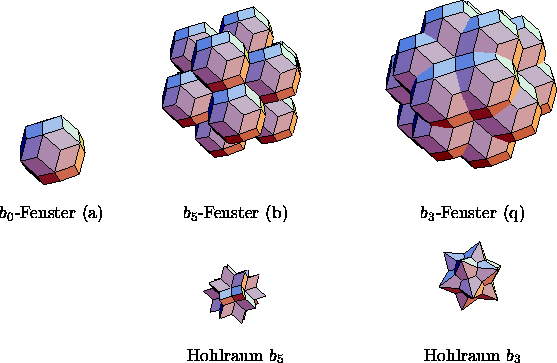
Abbildung: Die Fenster für ![]() -,
-, ![]() - und
- und ![]() -Punkte sowie die
eingeschlossenen leeren Bereiche
-Punkte sowie die
eingeschlossenen leeren Bereiche
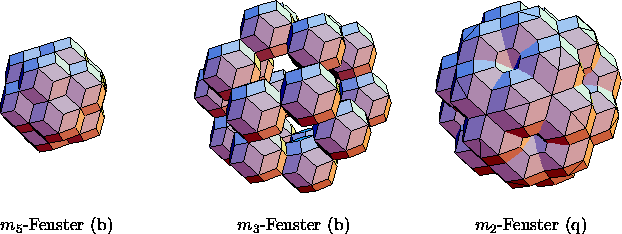
Abbildung: Die Fenster für ![]() -,
-, ![]() - und
- und ![]() -Punkte
-Punkte
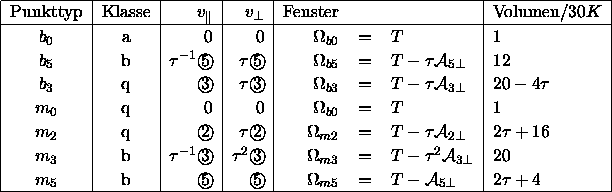
Tabelle 5.1: Die Fenster der verschiedenen Punkttypen
Das gesamte Quasigitter ![]() läßt sich als Vereinigung
der Gitter für
die Punktklassen a, b und q durch deren Fenster ausdrücken:
läßt sich als Vereinigung
der Gitter für
die Punktklassen a, b und q durch deren Fenster ausdrücken:
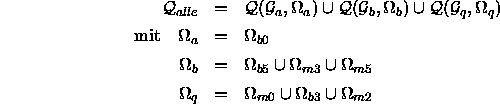
Die Fenster ![]() ,
, ![]() und
und ![]() sind in Abbildung
5.3 dargestellt.
sind in Abbildung
5.3 dargestellt.
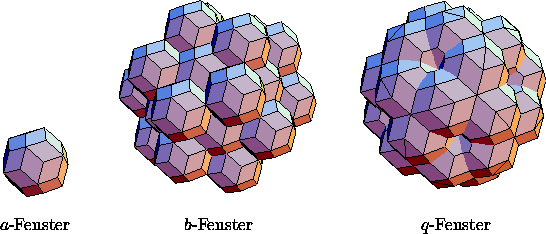
Abbildung: Die aufgebauten Fenster für a-, b- und q-Punktklassen