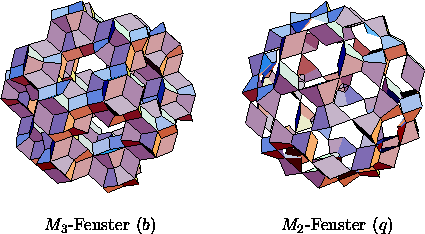
Abbildung 5.5: Die ``Nebel''-Fenster
Aus dem resultierenden Quasigitter müssen nun noch soviele Punkte
entfernt werden, daß es nicht zur Verletzung der Mindestabstände
kommt. Im Fenster betrifft dies die in Abbildung 5.5
gezeigten Bereiche. Eine Auswahl der Sekundärstruktur führt im Fenster
zu einer Wahrscheinlichkeitsdichte, ein Ensemble von möglichen Sekundärstrukturen zu einer über das Ensemble gemittelten Wahrscheinlichkeitsdichte.

Abbildung 5.5: Die ``Nebel''-Fenster
Die Auswahl der Punkte kann durch willkürliche Aufteilung des
Fensters in volle und leere Bereiche geschehen: auf diese Weise lassen
sich ![]() -
-![]() -Paare und
-Paare und ![]() -
-![]() -Paare leicht berücksichtigen:
Die Fenster werden jeweils in der Mitte flach abgeschnitten und die
äußere Hälfte leergelassen. Die resultierenden
-Paare leicht berücksichtigen:
Die Fenster werden jeweils in der Mitte flach abgeschnitten und die
äußere Hälfte leergelassen. Die resultierenden ![]() -Bereiche
werden für dominant über
-Bereiche
werden für dominant über ![]() -Bereiche erklärt, und man erhält
vollständig gefüllte Fenster, die die Mindestabstände (hard core
condition) einhalten. Dies sind genau die von Katz und Gratias
vorgeschlagenen Fenster (siehe Abschnitt 5 und
Abbildung 5.8). Allerdings ist hier eine
willkürliche Auswahl getroffen, die zu langreichweitigen
Korrelationen der Sekundärstruktur führt und damit Elsers
Vorstellung von einem statistischen Ensemble zuwiderläuft. Außerdem
sind so in jedem Mackaycluster nur im Mittel 7
-Bereiche erklärt, und man erhält
vollständig gefüllte Fenster, die die Mindestabstände (hard core
condition) einhalten. Dies sind genau die von Katz und Gratias
vorgeschlagenen Fenster (siehe Abschnitt 5 und
Abbildung 5.8). Allerdings ist hier eine
willkürliche Auswahl getroffen, die zu langreichweitigen
Korrelationen der Sekundärstruktur führt und damit Elsers
Vorstellung von einem statistischen Ensemble zuwiderläuft. Außerdem
sind so in jedem Mackaycluster nur im Mittel 7 ![]() -Atome
vorhanden, und bei gewissen
-Atome
vorhanden, und bei gewissen ![]() -Alternativen ist keine der beiden
Positionen besetzt, da sie durch benachbarte
-Alternativen ist keine der beiden
Positionen besetzt, da sie durch benachbarte ![]() verboten sind. Die
verboten sind. Die
![]() -Häufigkeit ist bei Katz und Gratias, wie schon Elser bemerkte,
in der Tat niedriger als
in seinem Modell.
-Häufigkeit ist bei Katz und Gratias, wie schon Elser bemerkte,
in der Tat niedriger als
in seinem Modell.
Für eine wenig korrelierte Sekundärstruktur sollte man die Form der
Wahrscheinlichkeitsverteilung offen lassen. Sichere Aussagen können
allenfalls über die Gesamthäufigkeiten der Punkttypen gemacht
werden: Elser zufolge soll von zwei sich ausschließenden möglichen
![]() -Positionen genau eine besetzt werden. Wenn man die Punkte aus
einer Wahrscheinlichkeitsverteilung im Fenster gewinnen will, so muß
das Integral der Wahrscheinlichkeitsverteilung über das
-Positionen genau eine besetzt werden. Wenn man die Punkte aus
einer Wahrscheinlichkeitsverteilung im Fenster gewinnen will, so muß
das Integral der Wahrscheinlichkeitsverteilung über das ![]() -Fenster
die Hälfte des Fenstervolumens betragen. Dies ist eine notwendige,
nicht hinreichende Bedingung, da für Korrelationen noch unabhängig
zu sorgen ist. Bei den
-Fenster
die Hälfte des Fenstervolumens betragen. Dies ist eine notwendige,
nicht hinreichende Bedingung, da für Korrelationen noch unabhängig
zu sorgen ist. Bei den ![]() -Positionen gibt es drei Fälle:
gewöhnlich können um einen geraden Vertex 7 von 20
-Positionen gibt es drei Fälle:
gewöhnlich können um einen geraden Vertex 7 von 20 ![]() -Positionen
frei besetzt werden. Bei bestimmten Vertizes, nämlich solchen, an
die ein bzw. zwei flache Rhomboeder mit einer flachen Ecke anliegen,
sind 3 bzw. 6
-Positionen
frei besetzt werden. Bei bestimmten Vertizes, nämlich solchen, an
die ein bzw. zwei flache Rhomboeder mit einer flachen Ecke anliegen,
sind 3 bzw. 6 ![]() -Positionen schon als
-Positionen schon als ![]() festgelegt. Die Auswahl
beschränkt sich aufgrund der Verbote auf 4 aus 10 bzw. 1 aus 2. Im
ersten Fall muß das Integral der Wahrscheinlichkeitsdichte 7/20 des
Fenstervolumens betragen, in den anderen beiden Fällen analog. Die
Fenster dieser Sorten von Vertizes sind bekannt: Sie stellen eine
Unterteilung des kanonischen Triakontaeders (des
festgelegt. Die Auswahl
beschränkt sich aufgrund der Verbote auf 4 aus 10 bzw. 1 aus 2. Im
ersten Fall muß das Integral der Wahrscheinlichkeitsdichte 7/20 des
Fenstervolumens betragen, in den anderen beiden Fällen analog. Die
Fenster dieser Sorten von Vertizes sind bekannt: Sie stellen eine
Unterteilung des kanonischen Triakontaeders (des ![]() -Fensters) dar.
Bei der Konstruktion des
-Fensters) dar.
Bei der Konstruktion des ![]() -Fensters durch Verschiebungen des
-Fensters durch Verschiebungen des
![]() -Fensters überträgt sich die Zugehörigkeit zu einer
Vertexsorte (siehe Abbildung 5.7): Die fertigen,
abgeschnittene
-Fensters überträgt sich die Zugehörigkeit zu einer
Vertexsorte (siehe Abbildung 5.7): Die fertigen,
abgeschnittene ![]() -Fensterteile müssen nur in derselben Weise
unterteilt werden.
-Fensterteile müssen nur in derselben Weise
unterteilt werden.