Wir haben bis hierher die Annahme verfolgt, daß die Elektronen in
erster Linie um die Atomkerne lokalisiert sind und die
Molekülorbitale durch eine schwache Kopplung der Atomorbitale
entstehen. Nun wollen wir einen komplementären Lösungsansatz
betrachten, mit der entgegengesetzten Annahme, daß die Elektronen
sich in erster Linie frei im Cluster bewegen können und die atomaren
Potentiale eine leichte Störung darstellen. Mit diesem Weg, die
Reihenfolge der Orbitalenergien in ikosaedersymmetrischen Clustern
abzuschätzen, folge ich der Darstellung in [Schu75].
Wir betrachten die Einelektronenzustände der Valenzelektronen in
einem Pseudopotential. Das Pseudopotential enthält Terme, die die
Orthogonalisierung auf die Core-Zustände simulieren, was einer
starken Abschirmung der Kernladungen entspricht. Deshalb kann man das
Clusterpotential in erster Näherung als kugelsymmetrisch betrachten:
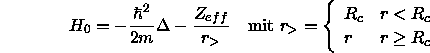
wobei 
der Radius einer Kugelschale ist, auf der die Summe der
effektiven
Kernladungen gleichmäßig verteilt sein soll.
Beim Bruch der Kugelsymmetrie durch einen kleinen
ikosaedersymmetrischen Störterm müssen als Orbitale Eigenzustände
zu irreduziblen Darstellungen der Ikosaedergruppe gewählt werden.
Dies geschieht, indem die irreduziblen Darstellungen der sphärischen
Drehgruppe als reduzible Darstellungen der Ikosaedergruppe aufgefaßt
und bezüglich dieser in irreduzible Darstellungen 
zerlegt werden. Für die Darstellungen und ihre
Dimensionen ergibt sich:
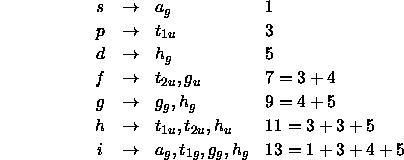
Die Termordnung für den obigen ungestörten Hamiltonoperator
ist in der linken Spalte der folgenden Tabelle zu sehen:
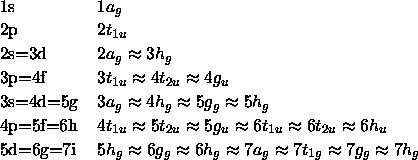
Falls der Störterm die Orbitalenergien verglichen mit der
l-Aufspaltung nur geringfügig verschiebt, ergibt sich mit der
ikosaedrischen Störung die in der rechten Spalte gezeigte Termordnung.
Für die Zustände niedriger Energie führt diese Methode auf
die gleiche Termordnung wie die Tight-Binding-Methode aus Abschnitt
6. Die energetisch niedrigsten Zustände des
Bergmanclusters in Abbildung 6.1 lassen sich
beispielsweise ihren Multiplizitäten nach indizieren als 
, was im Einklang mit der
hier abgeschätzten Reichenfolge ist.