Elsers Vorschrift läßt sich umformulieren als Dekoration der
beiden kanonischen Rhomboeder mit Atomen. Die Cluster, die ja auf den
Zellecken liegen, sind dabei schwer wiederzuerkennen. Eine
quasiperiodische Anordnung der beiden Zellen ergibt den Quasikristall.
Durch die Auszeichnung der geraden Vertizes und die Einbeschreibung
von Tetraedertiles fallen auch die Rhomboederflächen in zwei
Klassen: Flächen mit Tetraederkante als langer Diagonaler bzw. als
kurzer Diagonaler. Die Dekoration erhält die dreizähligen
Drehachsen von PR (lange Raumdiagonale) und OR (kurze Raumdiagonale).
Erst durch die Sekundärstruktur, die Auswahl der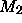 
- und
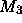-Positionen in den einzelnen Zellen des Quasikristalls wird die
Symmetrie gebrochen, wobei die Auswahl von Punkten in einer Zelle
unter Umständen
Entscheidungen für die benachbarten Zellen erzwingt bzw. verbietet.
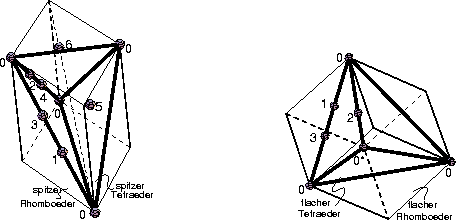
Abbildung: Repräsentative Atompositionen der Klasse q
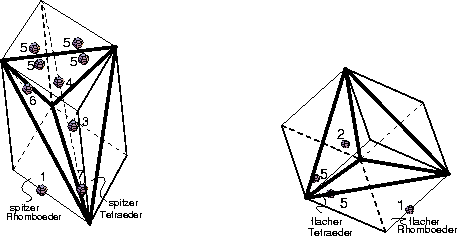
Abbildung: Repräsentative Atompositionen der Klasse b
Die Lagen repräsentativer Punkte in den Zellen sind in den Abbildungen 3.5 (Punkte der Klasse q) und 3.6 (Punkte der Klasse b) gezeigt. Geordnet nach den Punkttypen findet man folgende Fälle:
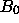: die Zentren der Bergmanatome besetzen die 'ungeraden' Vertizes,
also vier Ecken jedes Rhomboeders.
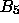: auf jeder Rhomboederkante sitzt ein 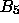-Atom (1 in Abb.
3.6) im Abstand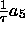 
zum 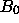-Atom am Kantenende. Außerdem gibt es sowohl im PR (3)
als auch im OR (2) je drei 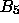, die symmetrisch bezüglich der
Drehachse liegen.
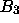: Auf jeder langen Tetraederkante, also jeder langen
Flächendiagonalen von geradem zu geradem Rhomboedervertex, liegen
zwei 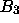(1, 3 in Abb. 3.5). Im PR gibt es ein
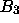auf der Drehachse (6) sowie drei 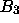symmetrisch zur
Drehachse (5). Auf kurzen Tetraederkanten, die in OR-Flächen
liegen, liegt ein weiteres 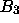-Atom (2). Der flache gerade Vertex des
OR (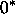
) ist ebenfalls ein 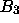-Punkt.
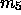-Atom, das nicht gleichzeitig 
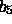ist, liegt im Inneren des
PR auf der Drehachse.
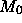: Die geraden Rhomboederecken (0) mit Ausnahme des oben
genannten 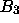auf der flachen Ecke des OR (0
).
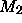: Auf jeder kurzen Flächendiagonalen des PR liegen zwei
mögliche 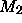-Plätze, die ``Splitpositionen'' (2,4, Abb.
3.5 links). Jeweils einer der beiden ist zu
besetzen. Bei den kurzen Flächendiagonalen des OR ist bereits ein
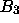-Atom (2, Abb. 3.5 rechts) festgelegt.
Treffen ein PR und ein OR mit solchen Flächen aufeinander, so
fällt das 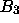auf einen der möglichen 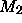-Plätze und
erzwingt so eine Auswahl.
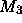: Im PR liegt ein 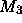auf der Drehachse (7 in Abbildung
3.6), drei sind symmetrisch darum angeordnet
(6). Außerdem enthält jede Fläche mit kurzer Diagonaler 4
mögliche 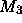-Plätze (5). Die Wahl eines der beiden 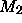auf
diese Fläche schließt 2 der 4 Plätze bereits aus, was
automatisch auf OR-Flächen der Fall ist. Die Auswahl in einer
Zelle hat starken Einfluß auf die benachbarten.