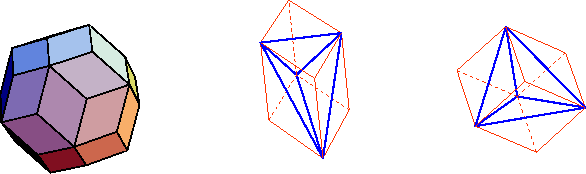
Abbildung 2.6: Triakontaeder, Rhomboeder und einbeschriebene Tetraeder

Abbildung 2.6: Triakontaeder, Rhomboeder und einbeschriebene Tetraeder
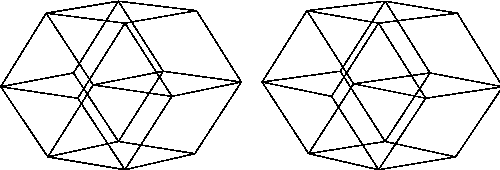
Abbildung 2.7: Der Simpletonvertex
Mit der im Anhang A beschriebene
cut-and-project-Methode und den obigen
Projektoren lassen sich aus den obigen Gitter verschiedene ``kanonische''
ikosaedrische Tilings gewinnen:
Bei Verwendung des primitiven Gitters ![]() ergibt sich das Rhomboedertiling [Kra84]. Das Fenster für
die Vertizes ist der schon von Kepler beschriebene rhombische
Triakontaeder (siehe Abbildung 2.6, links), die
Projektion der sechsdimensionalen Einheitszelle nach
ergibt sich das Rhomboedertiling [Kra84]. Das Fenster für
die Vertizes ist der schon von Kepler beschriebene rhombische
Triakontaeder (siehe Abbildung 2.6, links), die
Projektion der sechsdimensionalen Einheitszelle nach ![]() .
.
Er besitzt zweizählige Flächen sowie drei- und fünfzählige Ecken
mit Zentralabständen ![]() ,
, ![]() ,
, ![]() .
Die Kantenlänge beträgt
.
Die Kantenlänge beträgt ![]() , das Volumen
, das Volumen ![]() . Das
Rhomboedertiling besteht aus zwei Prototiles, einem spitzen (prolaten)
und einem flachen (oblaten) Rhomboeder, abgekürzt PR und OR, die in
Abbildung 2.6, Mitte und rechts, zu sehen sind. Ihre
Flächen sind Rauten mit Kantenlänge
. Das
Rhomboedertiling besteht aus zwei Prototiles, einem spitzen (prolaten)
und einem flachen (oblaten) Rhomboeder, abgekürzt PR und OR, die in
Abbildung 2.6, Mitte und rechts, zu sehen sind. Ihre
Flächen sind Rauten mit Kantenlänge ![]() und dem spitzen Winkel
arccos
und dem spitzen Winkel
arccos![]() , die Volumina betragen 3
, die Volumina betragen 3
![]() (PR) und 3
(PR) und 3 ![]() (OR) mit
(OR) mit ![]() . Die
Vertexkonfigurationen des idealen Tilings und ihre Häufigkeiten sind
in [Baa89] beschrieben. Das Tiling ist in einem gewissen Sinn
besonders unperiodisch, es kommt nämlich nie vor, daß zwei gleiche
Rhomboeder parallel aneinandergrenzen. Eine besonders häufige
Vertexkonfiguration, der sogenannte Simpletonvertex aus zwei PR und
zwei OR, ist in Abbildung 2.7 zu sehen. Durch
Spiegelung läßt sich ein Flip erzeugen, der zur Randomisierung eines
idealen Tilings dienen kann. Die Random Tilings können parallel
angrenzende Rhomboeder enthalten, besitzen aber (bis auf einige
Tilings, die im Ensemble eine Menge vom Maße 0
umfassen) immer noch scharfe Bragg-Reflexe im Beugungsbild.
. Die
Vertexkonfigurationen des idealen Tilings und ihre Häufigkeiten sind
in [Baa89] beschrieben. Das Tiling ist in einem gewissen Sinn
besonders unperiodisch, es kommt nämlich nie vor, daß zwei gleiche
Rhomboeder parallel aneinandergrenzen. Eine besonders häufige
Vertexkonfiguration, der sogenannte Simpletonvertex aus zwei PR und
zwei OR, ist in Abbildung 2.7 zu sehen. Durch
Spiegelung läßt sich ein Flip erzeugen, der zur Randomisierung eines
idealen Tilings dienen kann. Die Random Tilings können parallel
angrenzende Rhomboeder enthalten, besitzen aber (bis auf einige
Tilings, die im Ensemble eine Menge vom Maße 0
umfassen) immer noch scharfe Bragg-Reflexe im Beugungsbild.
Verwendet man dagegen das Gitter ![]() , so erhält man durch
Projektion der Voronoibegrenzungen P das Tiling
, so erhält man durch
Projektion der Voronoibegrenzungen P das Tiling ![]() ,
welches für diese Arbeit keine Rolle spielt,
und durch Projektion der dazu dualen Delonebegrenzungen
,
welches für diese Arbeit keine Rolle spielt,
und durch Projektion der dazu dualen Delonebegrenzungen ![]() das
Tetraedertiling
das
Tetraedertiling ![]() (siehe [Kra91]
sowie Anhang A). Das Tetraedertiling
(siehe [Kra91]
sowie Anhang A). Das Tetraedertiling ![]() wird, wie das Rhomboedertiling, durch den Triakontaeder
codiert. Seine Prototiles sind sechs verschiedene Tetraeder mit Kanten
in zweizähligen Richtungen, kurzen der Länge
wird, wie das Rhomboedertiling, durch den Triakontaeder
codiert. Seine Prototiles sind sechs verschiedene Tetraeder mit Kanten
in zweizähligen Richtungen, kurzen der Länge ![]() und langen der
Länge
und langen der
Länge ![]() . Als Seitenflächen ergeben sich gleichseitige und
``goldene'' Dreiecke. Die Vertizes des Tetraedertilings sind genau
die geraden Vertizes des Rhomboedertilings, das heißt, die Vertizes
mit gerader Summe der sechsdimensionalen Koordinaten. Die Kanten der
Tetraeder sind damit jeweils kurze oder lange Flächendiagonalen von
Rhomboedern. Das Rhomboedertiling ist aus dem Tetraedertiling
lokal ableitbar, zur lokalen Ableitbarkeit in umgekehrter Richtung
fehlt lokal die Information, welche Vertizes gerade und welche ungerade
sind.
. Als Seitenflächen ergeben sich gleichseitige und
``goldene'' Dreiecke. Die Vertizes des Tetraedertilings sind genau
die geraden Vertizes des Rhomboedertilings, das heißt, die Vertizes
mit gerader Summe der sechsdimensionalen Koordinaten. Die Kanten der
Tetraeder sind damit jeweils kurze oder lange Flächendiagonalen von
Rhomboedern. Das Rhomboedertiling ist aus dem Tetraedertiling
lokal ableitbar, zur lokalen Ableitbarkeit in umgekehrter Richtung
fehlt lokal die Information, welche Vertizes gerade und welche ungerade
sind.
Eine besondere Eigenschaft des ![]() -Tilings ist die
Zerschneidbarkeit (siehe [Kra91]): es gibt Ebenen besonders
hoher Vertexdichte senkrecht zu fünfzähligen Richtungen, die
vollständig von Tetraederflächen ausgefüllt sind. Diese bilden in
diesen Ebenen ein Tübinger Dreiecksmuster (siehe Abschnitt
2). die Ebenen treten wiederum in der Abfolge einer
Fibonaccikette auf (siehe [Kra92]). Der größte Teil aller
Vertizes liegt in solchen Ebenen.
-Tilings ist die
Zerschneidbarkeit (siehe [Kra91]): es gibt Ebenen besonders
hoher Vertexdichte senkrecht zu fünfzähligen Richtungen, die
vollständig von Tetraederflächen ausgefüllt sind. Diese bilden in
diesen Ebenen ein Tübinger Dreiecksmuster (siehe Abschnitt
2). die Ebenen treten wiederum in der Abfolge einer
Fibonaccikette auf (siehe [Kra92]). Der größte Teil aller
Vertizes liegt in solchen Ebenen.